《2025年书香天博暑假作业四年级数学北师大版西安出版社》

1. ( )形和( )形都是特殊的平行四边形。

答案： 长方　正方

2. 李明的身高是 1.45 米,王华的身高是 1.49 米,小强比李明高一些,比王华矮一些。小强的身高可能是( )米。

答案： 1.46（不唯一，只要大于1.45，小于1.49即可）

3. 将 38.46,163.4,4.386,68.43 按从小到大的顺序排列为( )＜( )＜( )＜( )。

答案： 解析：本题考察的是小数的大小比较。
比较小数大小时，先比较整数部分，整数部分大的小数就大；如果整数部分相同，再比较十分位，十分位上数字大的小数就大；如果十分位相同，就比较百分位，依次类推。
答案：4.386＜38.46＜68.43＜163.4。

4. 雕牌洗衣粉每袋 4.2 元,买 4 袋洗衣粉要( )元,42 元能买( )袋洗衣粉。

答案： 解析：本题考查的是利用乘法来解决实际问题以及总价、单价和数量之间的关系。
第一问要求买4袋洗衣粉的总价，根据总价=单价×数量，
将单价为4.2元，数量为4袋代入得：
$4.2 × 4 = 16.8(元)$。
第二问要求42元能买多少袋洗衣粉，根据数量=总价÷单价，
将总价为42元，单价为4.2元代入得：
$42 ÷ 4.2 = 10(袋)$。
答案：16.8；10。

5. 一瓶饮料 1000 克,一杯可装 125 克饮料,这瓶饮料可以倒( )杯。

答案： 解析：本题可根据除法的意义，用饮料的总质量除以每杯可装饮料的质量，得到可以倒的杯数。
计算过程：$1000÷125 = 8$（杯）
答案：8

1. 三角形按角分类为等边三角形、直角三角形和钝角三角形。 ( )

答案： 解析：三角形按角分类应分为直角三角形、锐角三角形和钝角三角形，而等边三角形是按边分类的一种特殊三角形，其三个角都是锐角，因此也属于锐角三角形的一种。题目中将等边三角形与直角三角形、钝角三角形并列作为三角形按角分类的类型是错误的。
答案：×

2. 5.6 米长的绳子和 5.60 米长的绳子一样长。 ( )

答案： 解析：根据小数的性质，小数的末尾添上“0”或去掉“0”小数的大小不变，所以$5.6$米=$5.60$米。
答案：√。

3. 一个正方形的草坪,边长是 40.1 米,张青沿着草坪四周走了一圈,他共走了 160.4 米。 ( )

答案： 解析：本题考查正方形周长的计算。
正方形的周长计算公式是：$周长 = 4 × 边长$。
根据题目，正方形的边长是 40.1 米，所以：
$周长 = 4 × 40.1 = 160.4(米)$。
张青沿着草坪四周走了一圈，他共走了 160.4 米，与计算结果相符。
答案：√。

4.

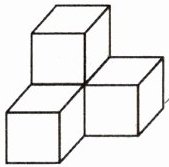
从正面和左面看到的形状不一样。 ( )

答案： 解析：从图中可以看出，从正面看有三层，第一层（最下面一层）有两个正方形，第二层和第三层各有一个正方形且在左侧；从左面看同样有三层，第一层有两个正方形，第二层和第三层各有一个正方形且在左侧，二者形状一样。
答案：×

5. 一个长方形的长是 15 米,宽是 x 米,周长是 52 米,可列方程 $ 15x = 52 $。 ( )

答案： 解析：根据长方形的周长公式，周长是两倍的长加两倍的宽，即 $2 × (15 + x) = 52$。题目中给出的方程 $15x = 52$ 显然是错误的，因为它没有正确应用周长公式。
答案：×。

1. 用 3、4、0 和小数点组成一个最小的小数是( )。

A.0.34
B.0.43
C.3.04

答案： 解析：要组成最小的小数，需要将数字从小到大排列，然后点上小数点。同时0不能放在整数的最高位。给定数字0、3、4，其中0最小，所以应将其放在小数点前一位，然后按照从小到大的顺序排列其余数字，得到0.34。比较选项，A为0.34，B为0.43，C为3.04，显然A是最小的。
答案：A。

2. 一个等边三角形的一条边长为 14 cm,它的周长是( )。

A.28 cm
B.42 cm
C.56 cm

答案： 等边三角形三条边长度相等，周长=边长×3。
14×3=42（cm）
答案：B.42 cm

3. 下列式子中,积大于任意一个乘数的是( )。

A.$ 1.28 × 0.45 $
B.$ 0.97 × 0.99 $
C.$ 1.23 × 3.01 $

答案： 解析：
本题考查的知识点是乘法运算中积与乘数的关系。
题目要求找出一个式子，其中的积大于任意一个乘数。
分析选项：
A. 对于 $1.28 × 0.45$，由于$0.45$小于$1$，所以积会小于$1.28$，不满足条件。
B. 对于 $0.97 × 0.99$，两个乘数都小于$1$，所以积也会小于任意一个乘数，不满足条件。
C. 对于 $1.23 × 3.01$，两个乘数都大于$0$，且其中一个乘数$3.01$大于$1$，另一个乘数$1.23$也大于$0$，因此积会大于任意一个乘数。
计算验证：
$1.23 × 3.01 = 3.7023$
积$3.7023$大于$1.23$且大于$3.01$的$1$倍（实际上只需关心是否大于其中一个乘数即可，这里同时大于两个乘数更说明了问题），满足题目要求。
答案：C。

4. 观察下面三个天平,第三个天平中缺少的重物的图形是( )。


A.□
B.△
C.△△

答案： 解析：本题可根据前两个天平的平衡关系，找出图形之间的重量关系，进而确定第三个天平中缺少的重物图形。
从第一个天平可知：$2$个$○$的重量等于$1$个$□$和$1$个$△$的重量之和，即$2○ = □ + △$ ①；
从第二个天平可知：$1$个$○$和$1$个$△$的重量等于$1$个$□$的重量，即$○ + △ = □$ ②；
将②式变形为$○=□ - △$，代入①式可得：
$2(□ - △)=□ + △$
$2□ - 2△=□ + △$
$2□ - □=△ + 2△$
$□ = 3△$
把$□ = 3△$代入②式可得：$○ + △ = 3△$，即$○ = 2△$。
再看第三个天平，左边是$1$个$○$和$1$个$□$，将$○ = 2△$，$□ = 3△$代入可得：左边重量为$2△ + 3△ = 5△$，右边已有$2$个$△$，所以还缺少$5△ - 2△ = 3△$，但图中右边已有一个$△$，所以缺少的重物图形是$2$个$△$，本题没有正确选项。若从选项本身分析，假设选项C表示$2$个$△$ ，则选C。
答案：假设选项C表示$2$个$△$ ，答案选C。