《2025年暑假作业四年级通用版西南师范大学出版社》

3. 妈妈买了一瓶香油,连瓶重 3.4 kg,用去一半后连瓶重 1.9 kg,这瓶香油原来有多少千克？瓶重多少千克？

答案： 油：3 kg 瓶：0.4 kg

4. 如图,在长 35 m、宽 14 m 的长方形地上有两条相交的小路,其余部分为草坪。请你算一算草坪的面积是多少平方米。

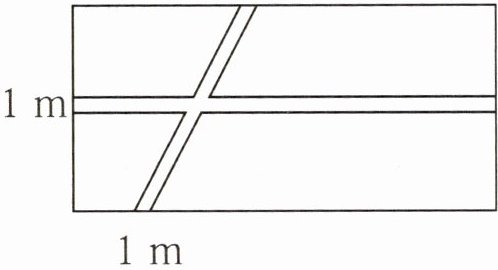
442

答案： 442 m²

灯球问题
《镜花缘》是清代李汝珍所著的长篇小说,书中描写了一位精通算学的才女“矶花仙子”，名叫米兰芬。米兰芬和众姐妹在宗伯府聚会,来到小鳌山楼上观灯。楼上的灯有两种,一种灯是上面 3 个大球,下缀 6 个小球,另一种灯是上面 3 个大球,下缀 18 个小球。楼下的灯也有两种,一种是 1 个大球缀 2 个小球,另一种是 1 个大球缀 4 个小球。知道楼上有大灯球 396 个,小灯球 1440 个;楼下有大灯球 360 个,小灯球 1200 个。才女们要米兰芬计算,楼上楼下的四种灯各有多少盏。你能算出来吗？

答案： 【解析】：
### 先计算楼上两种灯的数量
设上面$3$个大球，下缀$6$个小球的灯有$x$盏；上面$3$个大球，下缀$18$个小球的灯有$y$盏。
**根据大灯球数量列方程**：
已知每个第一种灯和第二种灯都有$3$个大球，且楼上大灯球有$396$个，可得到方程$3x + 3y=396$，化简为$x + y = 132$，即$x=132 - y$。
**根据小灯球数量列方程**：
第一种灯每个有$6$个小球，第二种灯每个有$18$个小球，且楼上小灯球有$1440$个，可得到方程$6x + 18y = 1440$。
**将$x = 132 - y$代入$6x + 18y = 1440$求解**：
把$x = 132 - y$代入$6x + 18y = 1440$中，得到$6×(132 - y)+18y = 1440$。
去括号得：$792-6y + 18y = 1440$。
合并同类项得：$792 + 12y = 1440$。
移项得：$12y=1440 - 792$，即$12y = 648$。
解得$y = 54$。
**把$y = 54$代入$x = 132 - y$求$x$的值**：
$x=132 - 54 = 78$。
### 再计算楼下两种灯的数量
设$1$个大球缀$2$个小球的灯有$m$盏；$1$个大球缀$4$个小球的灯有$n$盏。
**根据大灯球数量列方程**：
已知每个第一种灯和第二种灯都有$1$个大球，且楼下大灯球有$360$个，可得到方程$m + n = 360$，即$m = 360 - n$。
**根据小灯球数量列方程**：
第一种灯每个有$2$个小球，第二种灯每个有$4$个小球，且楼下小灯球有$1200$个，可得到方程$2m+4n = 1200$。
**将$m = 360 - n$代入$2m + 4n = 1200$求解**：
把$m = 360 - n$代入$2m + 4n = 1200$中，得到$2×(360 - n)+4n = 1200$。
去括号得：$720-2n + 4n = 1200$。
合并同类项得：$720 + 2n = 1200$。
移项得：$2n=1200 - 720$，即$2n = 480$。
解得$n = 240$。
**把$n = 240$代入$m = 360 - n$求$m$的值**：
$m=360 - 240 = 120$。
【答案】：楼上上面$3$个大球，下缀$6$个小球的灯有$78$盏，上面$3$个大球，下缀$18$个小球的灯有$54$盏；楼下$1$个大球缀$2$个小球的灯有$120$盏，$1$个大球缀$4$个小球的灯有$240$盏。