《2025年长江暑假作业四年级数学崇文书局》

1.(★★☆☆☆)判断对错。(对的打“√”,错的打“×”)
(1)4.06保留一位小数约是4。 ()
(2)3.05和3.058保留一位小数都是3.1。 ()
(3)近似数为8.43的三位小数不止一个。 ()
(4)大于0.5小于1的小数有5个。 ()
(5)因为$\triangle +\square =\bigcirc $,所以$\square -\triangle =\bigcirc $。 ()

答案：
(1)×；
(2)√；
(3)√；
(4)×；
(5)×

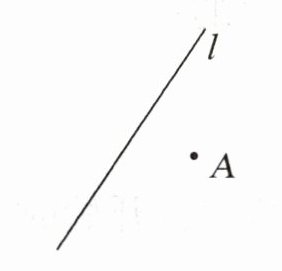
2.(★☆☆☆☆)画一画。过点A画直线l的垂线和平行线。

答案： 按照上述步骤画出过点$A$的直线$l$的垂线和平行线（具体图形需根据实际操作绘制）。

3.(★★★☆☆)求出下面图形中各个角的度数。
(1)我是等腰三角形, (2)我是直角三角形,有一个
底角是$50^{\circ }$。 内角是$60^{\circ }$。

答案： 本题可根据三角形内角和为$180^{\circ}$以及等腰三角形、直角三角形的性质来求解各个角的度数。
### $(1)$ 求等腰三角形各个角的度数
- **等腰三角形的性质**：等腰三角形的两个底角相等。
- **计算顶角的度数**：
已知该等腰三角形底角是$50^{\circ}$，根据三角形内角和是$180^{\circ}$，可得顶角的度数为$180^{\circ}-50^{\circ}-50^{\circ}=80^{\circ}$。
所以，该等腰三角形的三个角分别是$50^{\circ}$，$50^{\circ}$，$80^{\circ}$。
### $(2)$ 求直角三角形各个角的度数
- **直角三角形的性质**：直角三角形有一个角是$90^{\circ}$。
- **计算另一个锐角的度数**：
已知该直角三角形有一个内角是$60^{\circ}$，根据三角形内角和是$180^{\circ}$，可得另一个锐角的度数为$180^{\circ}-90^{\circ}-60^{\circ}=30^{\circ}$。
所以，该直角三角形的三个角分别是$90^{\circ}$，$60^{\circ}$，$30^{\circ}$。
综上，答案依次为：$(1)$ $\boldsymbol{50^{\circ}}$，$\boldsymbol{50^{\circ}}$，$\boldsymbol{80^{\circ}}$；$(2)$ $\boldsymbol{90^{\circ}}$，$\boldsymbol{60^{\circ}}$，$\boldsymbol{30^{\circ}}$。