第14页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
5 计算下面立体图形的体积。下面是三名同学分别给出的三种计算方法,谁的方法正确?请在该同学名字后面的□里画“√”。

丽丽 □ $3.14\times3^{2}\times6+\frac{1}{3}\times3.14\times3^{2}\times6$
明明 □ $3.14\times3^{2}\times6\times(1+\frac{1}{3})$
乐乐 □ $3.14\times3^{2}\times(6 + 6)$

丽丽 □ $3.14\times3^{2}\times6+\frac{1}{3}\times3.14\times3^{2}\times6$
明明 □ $3.14\times3^{2}\times6\times(1+\frac{1}{3})$
乐乐 □ $3.14\times3^{2}\times(6 + 6)$
答案:
丽丽√ 明明√
6 计算下面各立体图形的体积。
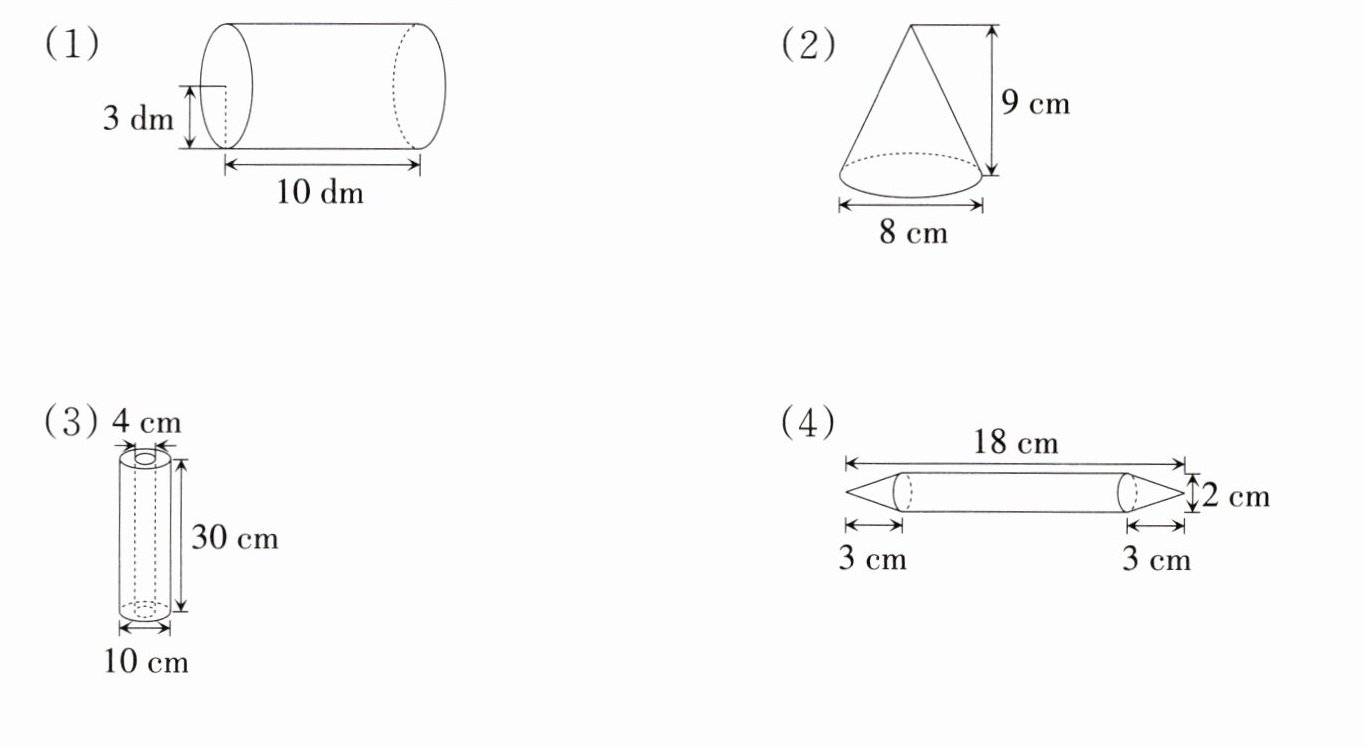

答案:
(1)$3.14×3²×10 = 282.6$ ($dm³$)
(2)$\frac{1}{3}×3.14×(8÷2)²×9 = 150.72$ ($cm³$)
(3)$3.14×(10÷2)²×30 - 3.14×(4÷2)²×30 = 1978.2$ ($cm³$)
(4)$3.14×(2÷2)²×(18 - 3 - 3)+\frac{1}{3}×3.14×(2÷2)²×3×2 = 43.96$ ($cm³$)
(1)$3.14×3²×10 = 282.6$ ($dm³$)
(2)$\frac{1}{3}×3.14×(8÷2)²×9 = 150.72$ ($cm³$)
(3)$3.14×(10÷2)²×30 - 3.14×(4÷2)²×30 = 1978.2$ ($cm³$)
(4)$3.14×(2÷2)²×(18 - 3 - 3)+\frac{1}{3}×3.14×(2÷2)²×3×2 = 43.96$ ($cm³$)
7 想一想,算一算。
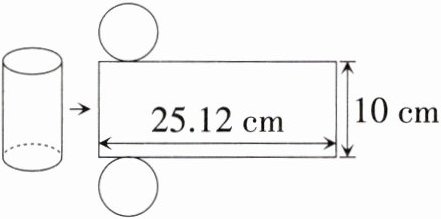
(1)下面是一个圆柱的展开图,求该圆柱的表面积和体积。
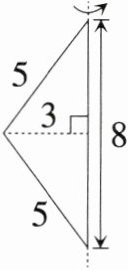
(2)求三角形绕轴旋转一周后形成的图形的体积。(单位:cm)
(1)下面是一个圆柱的展开图,求该圆柱的表面积和体积。

(2)求三角形绕轴旋转一周后形成的图形的体积。(单位:cm)

答案:
(1)表面积:$25.12×10 + 3.14×(25.12÷3.14÷2)²×2 = 351.68$ ($cm²$)
体积:$3.14×(25.12÷3.14÷2)²×10 = 502.4$ ($cm³$)
(2)$\frac{1}{3}×3.14×3²×8 = 75.36$ ($cm³$)
(1)表面积:$25.12×10 + 3.14×(25.12÷3.14÷2)²×2 = 351.68$ ($cm²$)
体积:$3.14×(25.12÷3.14÷2)²×10 = 502.4$ ($cm³$)
(2)$\frac{1}{3}×3.14×3²×8 = 75.36$ ($cm³$)
查看更多完整答案,请扫码查看


