《2025年王朝霞口算小达人六年级数学下册北师大版》

1 直接写出得数。
$2 - 0.75 =$　　　　$\frac{3}{4} + \frac{1}{6} =$　　　　$2.4×5 =$　　　　$3.14×400 =$
$45\%×2 =$　　　　$4÷\frac{1}{4} =$　　　　$5.6 + 3.4 =$　　　　$62.8÷3.14 =$
$\frac{3}{4}×\frac{5}{6} =$　　　　$\frac{5}{6} - \frac{2}{3} =$　　　　$\frac{2}{3} + \frac{1}{4} =$　　　　$3.14×30^{2} =$
$3.8÷0.01 =$　　　　$12×12 =$　　　　$\frac{3}{4}÷\frac{3}{5} =$　　　　$0.314÷3.14 =$
$0.45÷90\% =$　　　　$\frac{3}{22}×\frac{11}{18} =$　　　　$\frac{5}{11}÷\frac{15}{22} =$　　　　$\frac{1}{3}×3.14×12 =$

答案： $1.25$，$\frac{11}{12}$，$12$，$1256$
$0.9$，$16$，$9$，$20$
$\frac{5}{8}$，$\frac{1}{6}$，$\frac{11}{12}$，$2826$
$380$，$144$，$\frac{5}{4}$，$0.1$
$0.5$，$\frac{1}{12}$，$\frac{2}{3}$，$12.56$

2 脱式计算。
$\frac{3}{5}÷\frac{4}{9}×\frac{5}{7}$　　　　$8.5 - (5.6 + 4.8)÷1.3$　　　　$\frac{8}{9}÷[(\frac{1}{2} + \frac{2}{3})÷\frac{3}{4}]$

答案： $\frac{27}{28}$，$0.5$，$\frac{4}{7}$

3 求各圆锥的体积。
(1)$S = 7\ cm^{2}$　　　　(2)$C = 31.4\ dm$　　　　(3)$d = 3\ m$
$h = 9\ cm$　　　　　　$h = 6\ dm$　　　　　　$h = 4\ m$
$V = (\ \ \ \ \ )cm^{3}$　　　　$V = (\ \ \ \ \ )dm^{3}$　　　　$V = (\ \ \ \ \ )m^{3}$

答案：
(1)$21$
(2)$157$
(3)$9.42$

4 课内应用 如图所示，把一个底面积是$10\ dm^{2}$、高是$6\ dm$的圆柱形木料，削成一个由两个相对的圆锥组成的玩具。每个圆锥的高是原来圆柱高的一半，底面积和原来圆柱的底面积相等。削去部分的体积是(　　　　)$dm^{3}$，这个玩具的体积是(　　　　)$dm^{3}$。

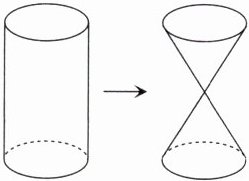
答案： $40$，$20$