【题目】用小立方块搭成的几何体,主视图和俯视图如下,

![]() 填空:这样的几何体有________种可能,它最多需要________小立方块,最少需要________小立方块.
填空:这样的几何体有________种可能,它最多需要________小立方块,最少需要________小立方块.
![]() 请画出最多和最少时的左视图.
请画出最多和最少时的左视图.
参考答案:
【答案】3 8 7
【解析】
(1)易得这个几何体共有3层,由俯视图可得第一层正方体的个数为4,由主视图可得第二层最多与最少的正方体的个数为3块,第三层只有一块,相加即可;(2)根据(1)分析得出左视图即可.
(1)由主视图可得:这个几何体共有3层,
由俯视图可得:第一层正方体的个数为4,由主视图可得第二层最少的正方体的个数为2块,第三层只有一块,此时第2列上面一个可前可后,
有个数相同的两种,故:最少为3+3+1=7个小立方块.
第一层正方体的个数为4,由主视图可得第二层最多的正方体的个数为3块,第三层只有一块,
故:最多为3+4+1=8个小立方块.
故这样的几何体有3种可能,
故答案为:3,8,7;
(2)如图所示:
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1是由若干个小圆圈堆成的一个形如等边三角形的图案,最上面一层有一个圆圈,
以下各层均比上一层多一个圆圈,一共堆了n 层.将图1倒置后与原图1拼成图2的形状,这样我们可以
算出图1中所有圆圈的个数为1+2+3+…+n=
 .
.
如果图中的圆圈共有13层,请解决下列问题:
(1)我们自上往下,在每个圆圈中按图3的方式填上一串连续的正整数1,2,3,4,……,则最底层最左
边这个圆圈中的数是 ;
(2)我们自上往下,在每个圆圈中按图4的方式填上一串连续的整数-23,-22,-21,-20,……,求
最底层最右边圆圈内的数是_______;
(3)求图4中所有圆圈中各数的绝对值之和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级有500名学生,从中随机抽取了一部分学生,统计每晚写作业的时间,根据它们的时间(单位:分钟),绘制出如下的统计图①和图②请根据相关信息,解答下列问题:

(1)图①中m=________,n=________;
(2)求统计的这组数据的平均数、众数和中位数;
(3)根据样本数据,估计这500名学生中,时间为120分钟的约有多少学生?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
(1)小明总共剪开了几条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.
(3)小明说:已知这个长方体纸盒高为20 cm,底面是一个正方形,并且这个长方体纸盒所有棱长的和是880 cm,求这个长方体纸盒的体积.
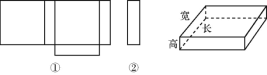
-
科目: 来源: 题型:
查看答案和解析>>【题目】古希腊著名的毕达哥拉斯学派把1,3,6,10…这样的数称为“三角形数”,而把1,4,9,16…这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是( )

A. 36=15+21 B. 25=9+16 C. 13=3+10 D. 49=18+31
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
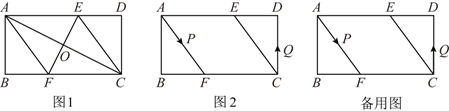
(1)如图1,连接AF、CE求证:四边形AFCE为菱形;
(2)如图1,求AF的长;
(3)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,点P的速度为每秒1cm,设运动时间为t秒.若点Q的速度为每秒0.8cm,当A、P、C、Q四点为顶点的四边形是平行四边形时,求t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】嘉淇同学用配方法推导一元二次方程ax2+bx+c=0(a≠0)的求根公式时,对于b2﹣4ac>0的情况,她是这样做的:
由于a≠0,方程ax2+bx+c=0变形为:
x2+
 x=﹣
x=﹣ ,…第一步
,…第一步x2+
 x+(
x+( )2=﹣
)2=﹣ +(
+( )2,…第二步
)2,…第二步(x+
 )2=
)2= ,…第三步
,…第三步x+
 =
= (b2﹣4ac>0),…第四步
(b2﹣4ac>0),…第四步x=
 ,…第五步
,…第五步嘉淇的解法从第 步开始出现错误;事实上,当b2﹣4ac>0时,方程ax2+bx+c=0(a≠O)的求根公式是 .
用配方法解方程:x2﹣2x﹣24=0.
相关试题

