【题目】如图,A(4,0),B(3,3),以AO,AB为边作平行四边形OABC,则经过C点的反比例函数的解析式为 . 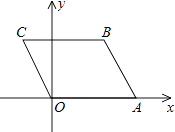
参考答案:
【答案】y=﹣ ![]()
【解析】解:设经过C点的反比例函数的解析式是y= ![]() (k≠0),设C(x,y).
(k≠0),设C(x,y).
∵四边形OABC是平行四边形,
∴BC∥OA,BC=OA;
∵A(4,0),B(3,3),
∴点C的纵坐标是y=3,|3﹣x|=4(x<0),
∴x=﹣1,
∴C(﹣1,3).
∵点C在反比例函数y= ![]() (k≠0)的图象上,
(k≠0)的图象上,
∴3= ![]() ,
,
解得,k=﹣3,
∴经过C点的反比例函数的解析式是y=﹣ ![]() .
.
所以答案是:y=﹣ ![]() .
.
【考点精析】认真审题,首先需要了解平行四边形的性质(平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分).
-
科目: 来源: 题型:
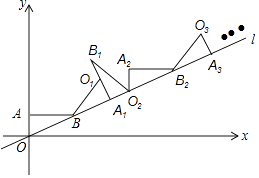
查看答案和解析>>【题目】如图,直线l经过平面直角坐标系的原点O,且与x轴正方向的夹角是30°,点A的坐标是(0,1),点B在直线l上,且AB∥x轴,则点B的坐标是 , 现将△ABO绕点B顺时针旋转到△A1BO1的位置,使点A的对应点A1落在直线l上,再将△A1BO1绕点A1顺时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线l上,顺次旋转下去…,则点A6的横坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线Y=ax2+bx一3与X轴相交于A(一1,0),B(3,0),P为抛物线上第四象限上的点.
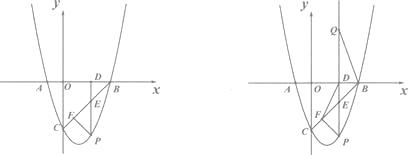
(1)求该抛物线的函数关系式.
(2)过点P作PD⊥X轴于点D,PD交BC于点E,当线段PE的长度最大时,求点P的坐标.
(3)当线段PE的长度最大时,作PF ⊥BC于点F,连结DF.在射线PD上有一点Q,满足∠PQB=∠DFB,问在坐标轴上是否存在一点R,使得S△RBE=S△QBE;如果存在,直接写出R点的坐标;如果不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c的图象如图所示,下列说法①a>0;②b2﹣4ac>0;③4a+2b+c>0;④c<0;⑤b>0.其中正确的有( )
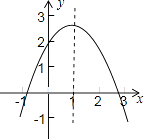
A.2个
B.3个
C.4个
D.5个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在
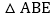 中,
中,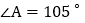 ,AE的垂直平分线MN交BE于点C,且
,AE的垂直平分线MN交BE于点C,且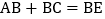 ,则
,则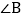 的度数是______.
的度数是______.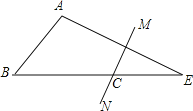
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学兴趣小组在活动时,老师提出了这样一个问题:如图1,在
 中,
中,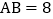 ,
,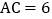 ,D是BC的中点,求BC边上的中线AD的取值范围.
,D是BC的中点,求BC边上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD到E,使
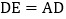 ,请补充完整证明“
,请补充完整证明“ ≌
≌ ”的推理过程.
”的推理过程.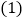 求证:
求证: ≌
≌
证明:
 延长AD到点E,使
延长AD到点E,使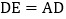
在
 和
和 中
中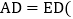 已作
已作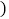 ,
,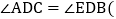 ______
______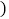 ,
,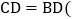 中点定义
中点定义 ,
, ≌
≌ ______
______ ,
, 探究得出AD的取值范围是______;
探究得出AD的取值范围是______;(感悟)解题时,条件中若出现“中点”“中线”等字样,可以考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.
(问题解决)
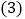 如图2,
如图2,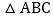 中,
中, ,
,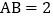 ,AD是
,AD是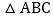 的中线,
的中线, ,
,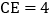 ,且
,且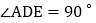 ,求AE的长.
,求AE的长.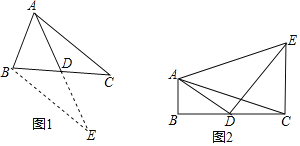
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,铁路上A、B两点相距25km,C、D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C、D两村到E站的距离相等,则E站应建在距A站多少千米处?

相关试题

