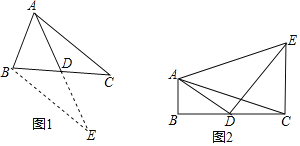
【题目】数学兴趣小组在活动时,老师提出了这样一个问题:如图1,在![]() 中,
中,![]() ,
,![]() ,D是BC的中点,求BC边上的中线AD的取值范围.
,D是BC的中点,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD到E,使![]() ,请补充完整证明“
,请补充完整证明“![]() ≌
≌![]() ”的推理过程.
”的推理过程.
![]() 求证:
求证:![]() ≌
≌![]()
证明:![]() 延长AD到点E,使
延长AD到点E,使![]()
在![]() 和
和![]() 中
中![]() 已作
已作![]() ,
,
![]() ______
______![]() ,
,
![]() 中点定义
中点定义![]() ,
,
![]() ≌
≌![]() ______
______![]() ,
,
![]() 探究得出AD的取值范围是______;
探究得出AD的取值范围是______;
(感悟)解题时,条件中若出现“中点”“中线”等字样,可以考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.
(问题解决)
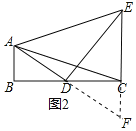
![]() 如图2,
如图2,![]() 中,
中,![]() ,
,![]() ,AD是
,AD是![]() 的中线,
的中线,![]() ,
,![]() ,且
,且![]() ,求AE的长.
,求AE的长.
参考答案:
【答案】![]() 见解析;
见解析;![]() 1<AD<7;
1<AD<7;![]() AE=6.
AE=6.
【解析】
(1)延长AD到点E,使DE=AD,根据SAS定理证明△ADC≌△EDB;
(2)根据全等三角形的性质、三角形的三边关系计算;
(3)延长AD交EC的延长线于F,证明△ABD≌△FCD,根据全等三角形的性质解答.
![]() 延长AD到点E,使
延长AD到点E,使![]() ,
,
在![]() 和
和![]() 中,
中,
![]() 已作
已作![]() ,
,
![]() 对顶角相等
对顶角相等![]() ,
,
![]() 中点定义
中点定义![]() ,
,
![]() ≌
≌![]() ,
,
故答案为:对顶角相等,SAS;
![]() ≌
≌![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
故答案为:![]() ;
;
![]() 延长AD交EC的延长线于F,
延长AD交EC的延长线于F,
![]() ,
,![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
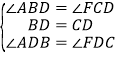 ,
,
![]() ≌
≌![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c的图象如图所示,下列说法①a>0;②b2﹣4ac>0;③4a+2b+c>0;④c<0;⑤b>0.其中正确的有( )
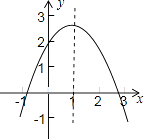
A.2个
B.3个
C.4个
D.5个 -
科目: 来源: 题型:
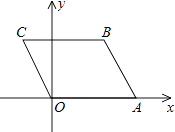
查看答案和解析>>【题目】如图,A(4,0),B(3,3),以AO,AB为边作平行四边形OABC,则经过C点的反比例函数的解析式为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在
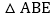 中,
中,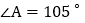 ,AE的垂直平分线MN交BE于点C,且
,AE的垂直平分线MN交BE于点C,且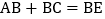 ,则
,则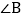 的度数是______.
的度数是______.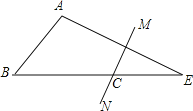
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,铁路上A、B两点相距25km,C、D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C、D两村到E站的距离相等,则E站应建在距A站多少千米处?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上有A、B、C三个点对应的数分别是a、b、c,且满足|a+24|+|b+10|+(c-10)2=0;动点P从A出发,以每秒1个单位的速度向终点C移动,设移动时间为t秒.
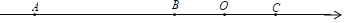
(1)求a、b、c的值;
(2)若点P到A点距离是到B点距离的2倍,求点P的对应的数;
(3)当点P运动到B点时,点Q从A点出发,以每秒2个单位的速度向C点运动,Q点到达C点后.再立即以同样的速度返回,运动到终点A,在点Q开始运动后第几秒时,P、Q两点之间的距离为8?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如下一组数:
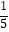 ,﹣
,﹣  ,
, 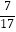 ,﹣
,﹣ 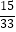 ,…,请用你发现的规律,猜想第2016个数为 .
,…,请用你发现的规律,猜想第2016个数为 .
相关试题

