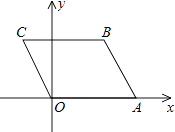
【题目】如图,直线l经过平面直角坐标系的原点O,且与x轴正方向的夹角是30°,点A的坐标是(0,1),点B在直线l上,且AB∥x轴,则点B的坐标是 , 现将△ABO绕点B顺时针旋转到△A1BO1的位置,使点A的对应点A1落在直线l上,再将△A1BO1绕点A1顺时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线l上,顺次旋转下去…,则点A6的横坐标是 . 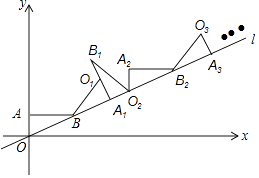
参考答案:
【答案】( ![]() ,1);
,1);![]() +
+ ![]() .
.
【解析】解:∵点A的坐标是(0,1),∠ABO=30°,AB∥x轴,
∴AB= ![]() ,AO=1,
,AO=1,
∴点B的坐标为( ![]() ,1),
,1),
由题可得,A1的横坐标为 ![]() +
+ ![]() ,
,
A2的横坐标为 ![]() +
+ ![]() ,
,
A3 3+ ![]() ,
,
A4的横坐标为3+3 ![]() ,
,
A5的横坐标为 ![]() +4
+4 ![]() ,
,
A6的横坐标为 ![]() +
+ ![]() ,
,
所以答案是:( ![]() ,1),
,1), ![]() +
+ ![]() .
.
【考点精析】本题主要考查了锐角三角函数的定义的相关知识点,需要掌握锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)如图,在直角坐标系xOy中,A(﹣1,0),B(3,0),将A,B同时分别向上平移2个单位,再向右平移1个单位,得到的对应点分别为D,C,连接AD,BC.

(1)直接写出点C,D的坐标:C ,D ;
(2)四边形ABCD的面积为 ;
(3)点P为线段BC上一动点(不含端点),连接PD,PO.求证:∠CDP+∠BOP=∠OPD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 如图,点P是菱形ABCD的对角线BD上的一动点,连接CP并延长交AD于E,交BA的延长线于点F.
如图,点P是菱形ABCD的对角线BD上的一动点,连接CP并延长交AD于E,交BA的延长线于点F.
(1)求证:△APD≌△CPD.
(2)当菱形ABCD变为正方形,且PC=2,tan∠PFA= 时,求正方形ABCD的边长.
时,求正方形ABCD的边长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b,c为△ABC的三条边的长,且满足b2+2ab=c2+2ac.
(1)试判断△ABC的形状,并说明理由;
(2)若a=6,b=5,求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线Y=ax2+bx一3与X轴相交于A(一1,0),B(3,0),P为抛物线上第四象限上的点.
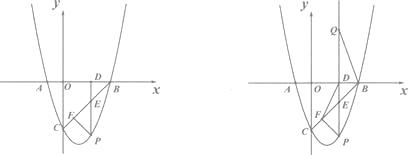
(1)求该抛物线的函数关系式.
(2)过点P作PD⊥X轴于点D,PD交BC于点E,当线段PE的长度最大时,求点P的坐标.
(3)当线段PE的长度最大时,作PF ⊥BC于点F,连结DF.在射线PD上有一点Q,满足∠PQB=∠DFB,问在坐标轴上是否存在一点R,使得S△RBE=S△QBE;如果存在,直接写出R点的坐标;如果不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c的图象如图所示,下列说法①a>0;②b2﹣4ac>0;③4a+2b+c>0;④c<0;⑤b>0.其中正确的有( )
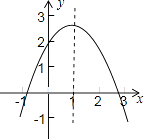
A.2个
B.3个
C.4个
D.5个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A(4,0),B(3,3),以AO,AB为边作平行四边形OABC,则经过C点的反比例函数的解析式为 .
相关试题

