【题目】如图,AB为⊙O的直径,直线CD切⊙O于点D,AM⊥CD于点M,连接AD,BD.
(1)求证:∠ADC=∠ABD;
(2)若AD=2![]() ,⊙O的半径为3,求MD的长.
,⊙O的半径为3,求MD的长.

参考答案:
【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)连接OD,由切线的性质和圆周角定理即可得到结果;
(2)由已知条件证得△ADM∽△ABD,即可得到结论.
试题解析:(1)连接OD,如图:

∵直线CD切⊙O于点D,∴∠CDO=90°,
∵AB为⊙O的直径,∴∠ADB=90°,
∴∠ADC+∠ADO=∠ADO+∠ODB=90°,∴∠ADC=∠ODB,
∵OB=OD,∴∠ODB=∠ADB,
∴∠ADC=∠ABD; …………5分
(2)∵⊙O的半径为3,AB=6,
∵∠ADB=90°,∴DB═![]() ,
,
∵∠AMD=∠ADB=90°,∠ADC=∠ABD,
∴△ADM∽△ABD,
∴![]() ,即
,即![]()
∴DM=2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一个密码系统,其原理如图:
输入x→2x→+5→输出
当输出11时,则输入的x=____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店的老板销售服装,他要以不低于进价120%的价格才能出售,但为了获得更多利润,他以高出进价80%的价格标价,若你想买下标价为360元的大衣,最多降价____元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国很多城市水资源缺乏,为了加强居民的节水意识,某市制定了每月用水4吨以内(包括4吨)和用水4吨以上两种收费标准(收费标准:每吨水的价格),某用户每月应交水费y(元)是用水量x(吨)的函数,其函数图象如图所示.
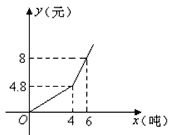
(1)分别求出当0≤x≤4、x>4时函数的解析式;
(2)当0≤x≤4、x>4时,每吨水的价格分别是多少?
(3)若某用户该月交水费12.8元,求该户用了多少吨水.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线AB:y=-x+b分别与x,y轴交于A(8,0)、B两点,过点B的直线交x轴轴负半轴于C,且OB:OC=4:3.
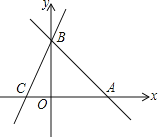
(1)求点B的坐标为 __________;
(2)求直线BC的解析式;
(3)动点M从C出发沿射线CA方向运动,运动的速度为每秒1个单位长度.设M运动t秒时,当t为何值时△BCM为等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“早穿皮袄,午穿纱,围着火炉吃西瓜.”这句谚语反映了我国新疆地区一天中,温度随时间变化而变化,其中自变量是______,因变量是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三角形ABC的三条边的长都是2个单位,现将三角形ABC沿射线BC方向向右平移1个单位后,得到三角形DEF,则四边形ABFD的周长为个单位.

相关试题

