【题目】直线AB:y=-x+b分别与x,y轴交于A(8,0)、B两点,过点B的直线交x轴轴负半轴于C,且OB:OC=4:3.
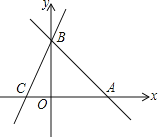
(1)求点B的坐标为 __________;
(2)求直线BC的解析式;
(3)动点M从C出发沿射线CA方向运动,运动的速度为每秒1个单位长度.设M运动t秒时,当t为何值时△BCM为等腰三角形.
参考答案:
【答案】(1)B(0,8);(2) y=![]() x+8;(3)10秒、
x+8;(3)10秒、![]() 秒或12秒.
秒或12秒.
【解析】试题分析:(1)把A的坐标代入y=-x+b,可得AB的解析式,令x=0,求出y的值,可得B的坐标;
(2)根据OB:OC=4:3,可得OC的长,根据待定系数法,可得函数解析式;
(3)根据等腰三角形的定义,分类讨论:MC=BC,MC=MB,BC=BM,①当MC=BC时,根据路程处以速度等于时间,可得答案;②当MC=MB时,根据两点间的距离,可得关于a的方程,根据解方程,可得a的值,再根据路程除以速度等于时间,可得答案;③当BC=BM时,根据线段垂直平分线的性质,可得MO的长,再根据两点间的距离,可得MC的长,根据路程除以速度等于时间,可得答案.
试题解析:解:(1)y=﹣x+b分别与x轴交于A(8、0),得:﹣8+b=0.解得b=8,即函数解析式为y=﹣x+8,当x=0时,y=8,B点坐标是(0,8);
(2)由OB:OC=4:3,BC=8,得:8:BC=4:3,解得BC=6,即C(﹣6,0),设直线BC的解析式为y=kx+b,图象经过点B,C,得: ![]() ,解得:
,解得: 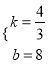 ,∴直线BC的解析式为y=
,∴直线BC的解析式为y=![]() x+8;
x+8;
(3)设M点坐标(a,0),由勾股定理得:BC=![]() =10,分三种情况讨论:
=10,分三种情况讨论:
①当MC=BC=10时,由路程处以速度等于时间,得10÷1=10(秒),即M运动10秒,△BCM为等腰三角形;
②当MC=MB时,MC2=MB2,即(a+6)2=a2+82,化简,得12a=28,解得a=![]() 即M(
即M(![]() ,0).MC=
,0).MC=![]() ﹣(﹣6)=
﹣(﹣6)=![]() +6=
+6=![]() ,由路程除以速度等于时间,得
,由路程除以速度等于时间,得![]() ÷1=
÷1=![]() (秒),即M运动
(秒),即M运动![]() 秒时,△BCM为等腰三角形;
秒时,△BCM为等腰三角形;
③当BC=BM时,得OC=OM=6,即MC=6﹣(﹣6)=6+6=12,由路程除以速度等于时间,得12÷1=12(秒),即M运动12秒时,△BCM为等腰三角形.
综上所述:t=10(秒),t=![]() (秒),t=12(秒)时,△BCM为等腰三角形.
(秒),t=12(秒)时,△BCM为等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店的老板销售服装,他要以不低于进价120%的价格才能出售,但为了获得更多利润,他以高出进价80%的价格标价,若你想买下标价为360元的大衣,最多降价____元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国很多城市水资源缺乏,为了加强居民的节水意识,某市制定了每月用水4吨以内(包括4吨)和用水4吨以上两种收费标准(收费标准:每吨水的价格),某用户每月应交水费y(元)是用水量x(吨)的函数,其函数图象如图所示.
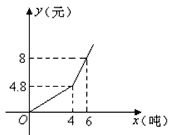
(1)分别求出当0≤x≤4、x>4时函数的解析式;
(2)当0≤x≤4、x>4时,每吨水的价格分别是多少?
(3)若某用户该月交水费12.8元,求该户用了多少吨水.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,直线CD切⊙O于点D,AM⊥CD于点M,连接AD,BD.
(1)求证:∠ADC=∠ABD;
(2)若AD=2
 ,⊙O的半径为3,求MD的长.
,⊙O的半径为3,求MD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“早穿皮袄,午穿纱,围着火炉吃西瓜.”这句谚语反映了我国新疆地区一天中,温度随时间变化而变化,其中自变量是______,因变量是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三角形ABC的三条边的长都是2个单位,现将三角形ABC沿射线BC方向向右平移1个单位后,得到三角形DEF,则四边形ABFD的周长为个单位.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知不等式组
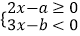 的整数解为1、2、3,如果把适合这个不等式组的整数a、b组成有序数对(a,b),那么对应在平面直角坐标系上的点共有的个数为 .
的整数解为1、2、3,如果把适合这个不等式组的整数a、b组成有序数对(a,b),那么对应在平面直角坐标系上的点共有的个数为 .
相关试题

