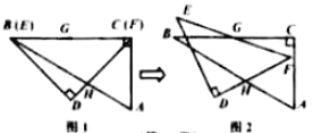
【题目】一副含![]() 和
和![]() 的三角板
的三角板![]() 和
和![]() 叠合在一起,边
叠合在一起,边![]() 与
与![]() 重合,
重合,![]() (如图1),点
(如图1),点![]() 为边
为边![]() 的中点,边
的中点,边![]() 与
与![]() 相交于点
相交于点![]() ,现将三角板
,现将三角板![]() 绕点
绕点![]() 按顺时针方向旋转(如图2),在
按顺时针方向旋转(如图2),在![]() 从
从![]() 到
到![]() 的变化过程中,观察点
的变化过程中,观察点![]() 的位置变化,点
的位置变化,点![]() 相应移动的路径长为 (结果保留根号).
相应移动的路径长为 (结果保留根号).
参考答案:
【答案】12![]() -18.
-18.
【解析】
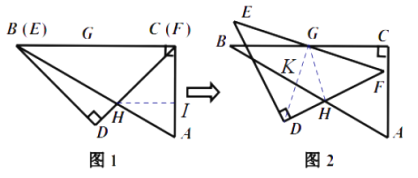
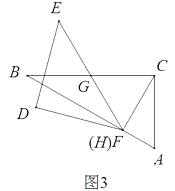
试题分析:如图2和图3,在 ∠ C G F 从 0 ° 到 60 ° 的变化过程中,点H先向AB方向移,在往BA方向移,直到H与F重合(下面证明此时∠CGF=60度),此时BH的值最大,如图3,当F与H重合时,连接CF,因为BG=CG=GF,所以∠BFC=90度,∵∠B=30度,∴∠BFC=60度,由CG=GF可得∠CGF=60度.∵BC=12cm,所以BF=![]() BC=6
BC=6![]() ;如图2,当GH⊥DF时,GH有最小值,则BH有最小值,且GF//AB,连接DG,交AB于点K,则DG⊥AB,∵DG=FG,∴∠DGH=45度,则KG=KH=
;如图2,当GH⊥DF时,GH有最小值,则BH有最小值,且GF//AB,连接DG,交AB于点K,则DG⊥AB,∵DG=FG,∴∠DGH=45度,则KG=KH=![]() GH=
GH=![]() ×(
×(![]() ×6
×6![]() )=3,BK=
)=3,BK=![]() KG=3
KG=3![]() ,则BH=BK+KH=3
,则BH=BK+KH=3![]() +3则点H运动的总路程为6
+3则点H运动的总路程为6![]() -(3
-(3![]() +3)+[12(
+3)+[12(![]() -1)-(3
-1)-(3![]() +3)]=12
+3)]=12![]() -18(cm).
-18(cm).
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在学习了一次方程(组)、一元一次不等式和一次函数后,把相关知识归纳整理如下:
一次函数与方程的关系:
①一次函数的解析式就是一个二元一次方程;
②点B的横坐标是方程①的解;
③点C的坐标(x,y)中的x,y的值是方程组②的解
一次函数与不等式的关系:
①函数y=kx+b的函数值y小于0时,自变量x的取值范围就是不等式③的解集;
②函数y=kx+b的函数值y大于0时,自变量x的取值范围就是不等式④的解集.
(1)请根据以上方框中的内容在下面数学序号后写出相应的式子:
①;②;③;④;
(2)如果点C的坐标为(2,5),那么不等式kx+b≥k1x+b1的解集是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】在等腰三角形中,其中两边分别为12、10.则周长为____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列关于函数
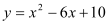 的四个命题:①当
的四个命题:①当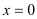 时,
时,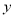 有最小值10;②
有最小值10;②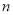 为任何实数,
为任何实数,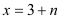 时的函数值大于
时的函数值大于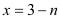 时的函数值;③若
时的函数值;③若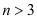 ,且
,且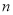 是整数,当
是整数,当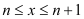 时,
时,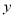 的整数值有
的整数值有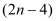 个;④若函数图象过点
个;④若函数图象过点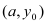 和
和 ,则
,则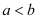 .其中真命题的序号是( )
.其中真命题的序号是( )A.① B.② C.③ D.④
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各式:
(1)1﹣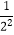
(2)(1﹣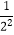 )(1﹣
)(1﹣ 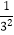 )
)
(3)(1﹣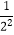 )(1﹣
)(1﹣ 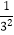 )(1﹣
)(1﹣ 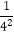 )
)
(4)请你根据上面算式所得的简便方法计算下式:
(1﹣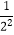 )(1﹣
)(1﹣ 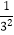 )(1﹣
)(1﹣ 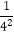 )…(1﹣
)…(1﹣ 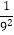 )(1﹣
)(1﹣ 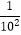 )…(1﹣
)…(1﹣ 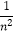 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】我们把能平分四边形面积的直线称为“好线”.利用下面的作图,可以得到四边形的“好线”:如图1四边形ABCD中,取对角线BD的中点O,连接OA,OC,显然,折线AOC能平分四边形ABCD的面积,再过点O作OE∥AC交CD于E,则直线AE即为一条“好线”.
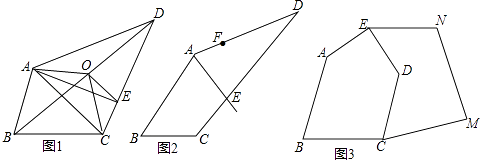
(1)如图1,试说明直线AE是“好线”的理由;
(2)如图2,AE为一条“好线”,F为AD边上的一点,请作出经过F点的“好线”,并说明理由;
(3)如图3,五边形ABCDE是一块土地的示意图,经过多年开垦荒地,现已变成如图3所示的形状,但原块土地与开垦荒地的分界小路(折线CDE)还保留着,现在请你过E点修一条直路.要求直路左边的土地面积与原来一样多(只需对作图适当说明无需说明理由) -
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:a2﹣4= .
相关试题

