【题目】已知,如图,∠1=∠ACB,∠2=∠3,FH⊥AB于H,求证:CD⊥AB.请将下面的推理过程补充完整.
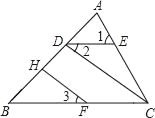
证明:FH⊥AB(已知)
∴∠BHF= °.( )
∵∠1=∠ACB(已知)
∴DE∥BC( )
∴∠2= .( )
∵∠2=∠3(已知)
∴∠3= .( )
∴CD∥FH( )
∴∠BDC=∠BHF= °.( )
∴CD⊥AB.
参考答案:
【答案】90,垂线定义;同位角相等,两直线平行;∠DCB,两直线平行, 内错角相等;∠DCB,等量代换;同位角相等,两直线平行;90;两直线平行, 同位角相等.
【解析】
根据平行线的判定得出DE∥BC,根据平行线的性质得出∠2=∠DCB,求出∠DCB=∠3,根据平行线的判定得出HF∥DC,根据平行线的性质得出∠FHB=∠CDB,即可得出答案.
解:证明:FH⊥AB(已知)
∴∠BHF= 90 °.( 垂线定义 )
∵∠1=∠ACB(已知)
∴DE∥BC(同位角相等,两直线平行 )
∴∠2= ∠DCB .( 两直线平行, 内错角相等 )
∵∠2=∠3(已知)
∴∠3= ∠DCB .( 等量代换 )
∴CD∥FH( 同位角相等,两直线平行 )
∴∠BDC=∠BHF= 90 °.(两直线平行, 同位角相等 )
∴CD⊥AB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形网格中,△DEF的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题:
(1)将△DEF向右平移5个单位长度,画出平移后的△D1E1F1;
(2) 将△DEF向上平移5个单位长度,再向右平移4个单位长度,画出平移后的△D2E2F2;
(3)求出三角形DEF的面积.
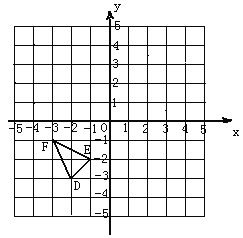
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面推理过程:
如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
∵∠1=∠2(已知),
且∠1=∠CGD( ),
∴∠2=∠CGD( ).
∴CE∥BF( ).
∴∠ =∠C( ).
又∵∠B=∠C(已知),
∴∠ =∠B(等量代换).
∴AB∥CD( ).
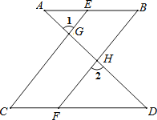
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在
 中,
中,  ,
,  ,将
,将 绕点
绕点 顺时针旋转
顺时针旋转 得
得 ,连接
,连接 、
、 .直线
.直线 、
、 交于点
交于点 .
.(
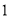 )当
)当 时,
时,  __________.
__________.(
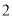 )在旋转过程中,四边形
)在旋转过程中,四边形 的面积是否存在最大值?若存在,求出最大值.若不存在,说明理由.
的面积是否存在最大值?若存在,求出最大值.若不存在,说明理由.(
 )如图②.若
)如图②.若 中,
中,  ,其余条件不变,四边形
,其余条件不变,四边形 的面积是否存在最大值?若存,求出最大值.若不存在,说明理由.
的面积是否存在最大值?若存,求出最大值.若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD边长为3,连接AC,AE平分∠CAD,交BC的延长线于点E,FA⊥AE,交CB延长线于点F,则EF的长为__________.

-
科目: 来源: 题型:
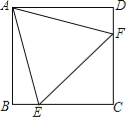
查看答案和解析>>【题目】如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=
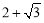 .
.其中正确的序号是 (把你认为正确的都填上).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
 的对角线交于点
的对角线交于点 点
点 ,
, 分别在
分别在 ,
, 上(
上( )且
)且 ,
, ,
, 的延长线交于点
的延长线交于点 ,
, ,
, 的延长线交于点
的延长线交于点 ,连接
,连接 .
.(1)求证:
 .
.(2)若正方形
 的边长为4,
的边长为4, 为
为 的中点,求
的中点,求 的长.
的长.
相关试题

