【题目】已知,直线![]() ,点
,点![]() 为平面内一点,连接
为平面内一点,连接![]() 与
与![]() .
.

(1)如图1,点![]() 在直线
在直线![]() 、
、![]() 之间,若
之间,若![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
(2)如图2,点![]() 在直线
在直线![]() 、
、![]() 之间,
之间,![]() 与
与![]() 的角平分线相交于点
的角平分线相交于点![]() ,写出
,写出![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
(3)如图3,点![]() 在直线
在直线![]() 下方,
下方,![]() 与
与![]() 的角平分线相交于点
的角平分线相交于点![]() ,直接写出
,直接写出![]() 与
与![]() 的数量关系.
的数量关系.
参考答案:
【答案】(1)∠APC=80°;(2)∠AKC=![]() ∠APC;(3)∠AKC=
∠APC;(3)∠AKC=![]() ∠APC.
∠APC.
【解析】
(1)先过P作PE∥AB,根据平行线的性质即可得到∠APE=∠BAP,∠CPE=∠DCP,再根据∠APC=∠APE+∠CPE=∠BAP+∠DCP进行计算即可;
(2)过K作KE∥AB,根据KE∥AB∥CD,可得∠AKE=∠BAK,∠CKE=∠DCK,进而得到∠AKC=∠AKE+∠CKE=∠BAK+∠DCK,同理可得,∠APC=∠BAP+∠DCP,再根据角平分线的定义,得出∠BAK+∠DCK=![]() ∠BAP+
∠BAP+![]() ∠DCP=
∠DCP=![]() (∠BAP+∠DCP)=
(∠BAP+∠DCP)=![]() ∠APC,进而得到∠AKC=
∠APC,进而得到∠AKC=![]() ∠APC;
∠APC;
(3)过K作KE∥AB,根据KE∥AB∥CD,可得∠BAK=∠AKE,∠DCK=∠CKE,进而得到∠AKC=∠AKE-∠CKE=∠BAK-∠DCK,同理可得,∠APC=∠BAP-∠DCP,再根据角平分线的定义,得出∠BAK-∠DCK=![]() ∠BAP-
∠BAP-![]() ∠DCP=
∠DCP=![]() (∠BAP-∠DCP)=
(∠BAP-∠DCP)=![]() ∠APC,进而得到∠AKC=
∠APC,进而得到∠AKC=![]() ∠APC.
∠APC.
(1)如图1,过P作PE∥AB,
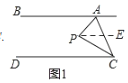
∵AB∥CD,
∴PE∥AB∥CD,
∴∠APE=∠BAP,∠CPE=∠DCP,
∴∠APC=∠APE+∠CPE=∠BAP+∠DCP=60°+20°=80°;
(2)∠AKC=![]() ∠APC.
∠APC.
理由:如图2,过K作KE∥AB,

∵AB∥CD,
∴KE∥AB∥CD,
∴∠AKE=∠BAK,∠CKE=∠DCK,
∴∠AKC=∠AKE+∠CKE=∠BAK+∠DCK,
过P作PF∥AB,
同理可得,∠APC=∠BAP+∠DCP,
∵∠BAP与∠DCP的角平分线相交于点K,
∴∠BAK+∠DCK=![]() ∠BAP+
∠BAP+![]() ∠DCP=
∠DCP=![]() (∠BAP+∠DCP)=
(∠BAP+∠DCP)= ![]() ∠APC,
∠APC,
∴∠AKC=![]() ∠APC;
∠APC;
(3)∠AKC=![]() ∠APC.
∠APC.
理由:如图3,过K作KE∥AB,

∵AB∥CD,
∴KE∥AB∥CD,
∴∠BAK=∠AKE,∠DCK=∠CKE,
∴∠AKC=∠AKE∠CKE=∠BAK∠DCK,
过P作PF∥AB,
同理可得,∠APC=∠BAP∠DCP,
∵∠BAP与∠DCP的角平分线相交于点K,
∴∠BAK∠DCK=![]() ∠BAP
∠BAP![]() ∠DCP=
∠DCP=![]() (∠BAP∠DCP)=
(∠BAP∠DCP)=![]() ∠APC,
∠APC,
∴∠AKC=![]() ∠APC.
∠APC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形 ABCD中,对角线 AC, BD交于点O,
(1)若AO=
 BD,求证:四边形 ABCD为矩形;
BD,求证:四边形 ABCD为矩形;(2) 若 AE BD于点E,CF BD于点F,求证:AE CF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】体育场上,老师用绳子围成一个周长为
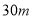 的游戏场地,围成的场地是如图所示的矩形
的游戏场地,围成的场地是如图所示的矩形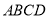 ,设
,设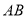 的长为
的长为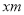 (
(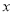 取整数),矩形
取整数),矩形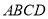 的面积为
的面积为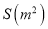 .
.⑴.写出
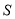 与
与 之间的函数关系式,求出
之间的函数关系式,求出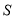 的最值和相应的
的最值和相应的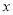 的值;
的值;⑵.若矩形
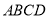 的面积为
的面积为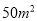 且
且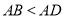 ,请求出此时
,请求出此时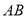 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,网格中的每一个小方格都是是边长为 1 个单位的正方形,只能使用无刻度直尺,请以格点为顶点按照以下要求作图:
(1)请在图 1 中画出ABC,其中AC=
 ,AB=
,AB= ,BC=
,BC= ;
;(2)请在图 2 中画出面积为 8 的正方形 ABCD,且找出点 O,使得经过点 O 的所有直线都平分正方形ABCD 的面积,保留作图痕迹.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了推动球类运动的普及,成立多个球类运动社团,为此,学生会采取抽样调查的方法,从足球、乒乓球、篮球、排球四个项目调查了若干名学生的兴趣爱好(要求每位同学只能选择其中一种自己喜欢的球类运动),并将调查结果绘制成了如下条形统计图和扇形统计图(不完整).请你根据图中提供的信息,解答下列问题:

(1)本次抽样调查,共调查了 名学生;
(2)请将条形统计图和扇形统计图补充完整;
(3)若该学校共有学生1800人,根据以上数据分析,试估计选择排球运动的同学约有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于
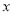 的一元二次方程
的一元二次方程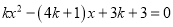 (
(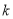 是整数).
是整数).⑴.求证:方程有两个不相等的实数根;
⑵.若方程的两个实数根分别为
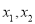 (其中
(其中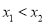 ),设
),设 ,判断
,判断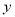 是否为变量
是否为变量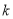 的函数?如果是,请写出函数表达式;若不是,请说明理由.
的函数?如果是,请写出函数表达式;若不是,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】“立定跳远”是我市初中毕业生体育测试项目之一.测试时,记录下学生立定跳远的成绩,然后按照评分标准转化为相应的分数,满分10分.其中男生立定跳远的评分标准如下:注:成绩栏里的每个范围,含最低值,不含最高值.
成绩(米)
…
1.80~1.86
1.86~1.94
1.94~2.02
2.02~2.18
2.18~2.34
2.34~
得分(分)
…
5
6
7
8
9
10
某校九年级有480名男生参加立定跳远测试,现从中随机抽取10名男生测试成绩(单位:分)如下:
1.96 2.38 2.56 2.04 2.34 2.17 2.60 2.26 1.87 2.32
请完成下列问题:
(1)求这10名男生立定跳远成绩的极差和平均数;
(2)求这10名男生立定跳远得分的中位数和众数;
(3)如果将9分(含9分)以上定为“优秀”,请你估计这480名男生中得优秀的人数.
相关试题

