【题目】在△ABC中,以AB为斜边,作直角△ABD,使点D落在△ABC内,∠ADB=90°.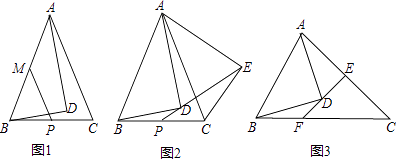
(1)如图1,若AB=AC,∠DBA=60°,AD=7 ![]() ,点P、M分别为BC、AB边的中点,连接PM,求线段PM的长;
,点P、M分别为BC、AB边的中点,连接PM,求线段PM的长;
(2)如图2,若AB=AC,把△ABD绕点A逆时针旋转一定角度,得到△ACE,连接ED并延长交BC于点P,求证:BP=CP;
(3)如图3,若AD=BD,过点D的直线交AC于点E,交BC于点F,EF⊥AC,且AE=EC,请直接写出线段BF、FC、AD之间的关系(不需要证明).
参考答案:
【答案】
(1)
解:如图1中,

∵∠ADB=90°,∠DBA=60°,AD=7 ![]() ,
,
∴∠BAD=30°,
∴AB=2BD,设BD=a,则AB=2a,
∵AB2=BD2+AD2,
∴(2a)2=a2+(7 ![]() )2,
)2,
∴a=7,
∴AB=AC=14,
∵AM=MB,PB=PC,
∴PM= ![]() AC=7
AC=7
(2)
证明:如图2中,在ED上截取EQ=DP,连接CQ.

∵AD=AE,
∴∠1=∠2,
∵∠ADB=∠AEC=90°,
∴∠1+∠3=90°,∠2+∠4=90°,
∴∠3=∠4,
∵BD=EC,
∴△EQC≌△DPB,
∴CQ=BP,∠QCE=∠DBP,
∵∠CQP=∠3+∠QCE,∠CPQ=∠4+∠DBP,
∴∠CQP=∠CPQ,
∴CQ=PC,
∴PB=PC.
(3)
解:结论:2AD2=FB2+CF2.
理由:如图3中,连接AF交BD于N,连接CD延长至H.

∵EA=EC,EF⊥AC,
∴DA=DC,
∵∠ADB=90°,DA=DB,
∴DA=DC=DB,∴∠DBA=∠DAB=45°,AB= ![]() AD,
AD,
∴∠DAC=∠DCA,∠DBC=∠DCB,
∵∠ADH=∠DAC+∠ACD,∠BDH﹣∠DBC+∠DCB,
∴∠ADB=2∠ACD+2∠DCB=90°,
∴∠ACF=45°,
∵FA=FC,
∴∠FAC=∠FCA=45°,
∴∠AFC=90°
∵∠AND=∠BNF,∠ADN=∠BFN=90°,
∴△AND∽△BNF,
∴ ![]() ,
,
∴ ![]() ,∵∠ANB=∠DNF,
,∵∠ANB=∠DNF,
∴△ANB∽△DNF,
∴∠DFN=∠ABD=45°,
∵FE⊥AC,AE=EC,
∴FA=FC,∠AFE=∠CFE=45°,
∴∠AFC=∠AFB=90°,
∴AB2=BF2+AF2,
∴2AD2=BF2+CF2
【解析】(1)根据直角三角形30度角性质求出AB,再根据三角形中位线定理即可求出PM.(2)如图2中,在ED上截取EQ=DP,连接CQ.首先证明△EQC≌△DPB,推出QC=PB,再证明QC=PC即可解决问题.(3)结论:2AD2=FB2+CF2 . 如图3中,连接AF交BD于N.由△AND∽△BNF,推出 ![]() ,推出
,推出 ![]() ,又∠ANB=∠DNF,推出△ANB∽△DNF,从∠DFN=∠ABD=45°,在RtABF中利用勾股定理即可证明.
,又∠ANB=∠DNF,推出△ANB∽△DNF,从∠DFN=∠ABD=45°,在RtABF中利用勾股定理即可证明.
【考点精析】根据题目的已知条件,利用勾股定理的概念和三角形中位线定理的相关知识可以得到问题的答案,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数轴是初中数学教材中数形结合的第一个实例,它包括原点,正方向和长度单位三要素,每一个实数都可以用数轴上的一个点来表示.
 数轴上某一个点所对应的数为
数轴上某一个点所对应的数为 ,另一个点对应的数为
,另一个点对应的数为 ,则这两点之间的距离为________;
,则这两点之间的距离为________; 数轴上的数
数轴上的数 对应的点为
对应的点为 ,点
,点 位于
位于 点的右边,距
点的右边,距 点
点 个长度单位,
个长度单位, 为线段
为线段 上的一点,
上的一点, ,电子蚂蚁
,电子蚂蚁 、
、 分别从
分别从 、
、 同时出发,相向而行,
同时出发,相向而行, 的速度为
的速度为 个长度单位/秒,
个长度单位/秒, 的速度为
的速度为 个长度单位/秒.
个长度单位/秒.①当
 、
、 距
距 点距离相同时,求运动时间
点距离相同时,求运动时间 ;
;②若电子蚂蚁
 通过
通过 点
点 秒后与电子蚂蚁
秒后与电子蚂蚁 相遇,求
相遇,求 的值.
的值.
-
科目: 来源: 题型:
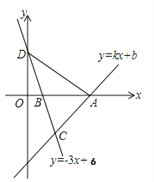
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象经过点A(8,0),直线y=-3x+6与x轴交于点B,与y轴交于点D,且两直线交于点C(4,m).
(1)求m的值及一次函数的解析式;
(2)求△ACD的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】出租车司机小李某天下午的营运全是在东西走向的人民大街上进行的.如果规定向东为正,向西为负,他这天下午行车里程(单位:千米)如下:
 ,
, ,
,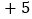 ,
,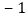 ,
,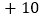 ,
,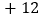 ,
,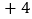 ,
, .
.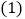 人民大街总长不小于________千米;
人民大街总长不小于________千米; 将最后一名乘客送往目的地时,小李距离下午出车时的出发点多远?
将最后一名乘客送往目的地时,小李距离下午出车时的出发点多远? 若出租车耗油量为每千米
若出租车耗油量为每千米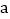 升,这天下午小李共耗油多少升?
升,这天下午小李共耗油多少升? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+2x+3与x轴交于A,B两点,与y轴交于点C,点D,C关于抛物线的对称轴对称,直线AD与y轴相交于点E.

(1)求直线AD的解析式;
(2)如图1,直线AD上方的抛物线上有一点F,过点F作FG⊥AD于点G,作FH平行于x轴交直线AD于点H,求△FGH周长的最大值;
(3)如图2,点M是抛物线的顶点,点P是y轴上一动点,点Q是坐标平面内一点,四边形APQM是以PM为对角线的平行四边形,点Q′与点Q关于直线AM对称,连接M Q′,P Q′.当△PM Q′与□APQM重合部分的面积是APQM面积的 时,求APQM面积.
时,求APQM面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】随着手机的普及,微信
 一种聊天软件
一种聊天软件 的兴起,许多人抓住这种机会,做起了“微商”,很多农产品也改变了原来的销售模式,实行了网上销售,这不刚大学毕业的小明把自家的冬枣产品也放到了网上,他原计划每天卖100斤冬枣,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况
的兴起,许多人抓住这种机会,做起了“微商”,很多农产品也改变了原来的销售模式,实行了网上销售,这不刚大学毕业的小明把自家的冬枣产品也放到了网上,他原计划每天卖100斤冬枣,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况 超额记为正,不足记为负
超额记为正,不足记为负 单位:斤
单位:斤 ;
;星期
一
二
三
四
五
六
日
与计划量的差值







(1)根据记录的数据可知前三天共卖出 ______ 斤;
(2)根据记录的数据可知销售量最多的一天比销售量最少的一天多销售 ______ 斤;
(3)本周实际销售总量达到了计划数量没有?
(4)若冬季每斤按8元出售,每斤冬枣的运费平均3元,那么小明本周一共收入多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】我校全体同学参加了二年级刘XX同学的捐款活动,随机抽查了部分同学捐款的情况统计如图所示.
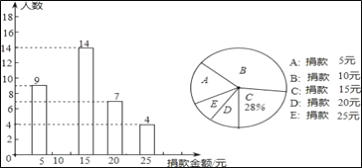
(1)本次共抽查学生 人,并将条形图补充完整;
(2)捐款金额的众数是 ,平均数是 ;
(3)在我校2200名学生中,捐款15元及以上(含15元)的学生估计有多少人?
相关试题

