【题目】数轴是初中数学教材中数形结合的第一个实例,它包括原点,正方向和长度单位三要素,每一个实数都可以用数轴上的一个点来表示.
![]() 数轴上某一个点所对应的数为
数轴上某一个点所对应的数为![]() ,另一个点对应的数为
,另一个点对应的数为![]() ,则这两点之间的距离为________;
,则这两点之间的距离为________;
![]() 数轴上的数
数轴上的数![]() 对应的点为
对应的点为![]() ,点
,点![]() 位于
位于![]() 点的右边,距
点的右边,距![]() 点
点![]() 个长度单位,
个长度单位,![]() 为线段
为线段![]() 上的一点,
上的一点,![]() ,电子蚂蚁
,电子蚂蚁![]() 、
、![]() 分别从
分别从![]() 、
、![]() 同时出发,相向而行,
同时出发,相向而行,![]() 的速度为
的速度为![]() 个长度单位/秒,
个长度单位/秒,![]() 的速度为
的速度为![]() 个长度单位/秒.
个长度单位/秒.
①当![]() 、
、![]() 距
距![]() 点距离相同时,求运动时间
点距离相同时,求运动时间![]() ;
;
②若电子蚂蚁![]() 通过
通过![]() 点
点![]() 秒后与电子蚂蚁
秒后与电子蚂蚁![]() 相遇,求
相遇,求![]() 的值.
的值.
![]()
参考答案:
【答案】(1)10; (2) ①![]() m或
m或![]() m;②30.
m;②30.
【解析】
(1)根据两点间的距离公式求解即可;(2)①根据P、Q距C点距离相同,列出方程可求时间t;②根据电子蚂蚁Q通过C点1秒后与电子蚂蚁P相遇,由时间的等量关系列出方程可求m的值.
:(1)2-(-8)=10.
故这两点之间的距离为10.
故答案为:10;
(2)①依题意有:![]() m-3t=
m-3t=![]() m-2t,
m-2t,
解得t=![]() m;
m;
或3t+2t=m,
解得t=![]() m.
m.
故运动时间t为![]() m或
m或![]() m.
m.
②依题意有:![]() ,
,
解得m=30.
故m的值为30.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一艘载重480 t的船,容积是1050 m3,现有甲种货物450 m3,乙种货物350 t,而甲种货物每吨体积2.5 m3,乙种货物每立方米0.5 t.问两种货物是否都能装上船? 如果不能,请说明理由,并求出为了最大限度地利用船的载重量和容积,两种货物应各装多少吨.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成。硬纸板以如图两种方式裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。

现有19张硬纸板,裁剪时
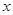 张用A方法,其余用B方法。
张用A方法,其余用B方法。(1)用
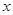 的代数式分别表示裁剪出的侧面和底面的个数;
的代数式分别表示裁剪出的侧面和底面的个数;(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点P、Q分别为BC、CD边上一点,且BP=CQ=
 BC,连接AP、BQ交于点G,在AP的延长线上取一点E,使GE=AG,连接BE、CE.∠CBE的平分线BN交AE于点N,连接DN,若DN=
BC,连接AP、BQ交于点G,在AP的延长线上取一点E,使GE=AG,连接BE、CE.∠CBE的平分线BN交AE于点N,连接DN,若DN= ,则CE的长为_____.
,则CE的长为_____.
-
科目: 来源: 题型:
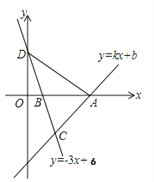
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象经过点A(8,0),直线y=-3x+6与x轴交于点B,与y轴交于点D,且两直线交于点C(4,m).
(1)求m的值及一次函数的解析式;
(2)求△ACD的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】出租车司机小李某天下午的营运全是在东西走向的人民大街上进行的.如果规定向东为正,向西为负,他这天下午行车里程(单位:千米)如下:
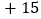 ,
,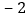 ,
,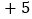 ,
,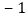 ,
,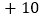 ,
,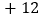 ,
,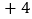 ,
, .
.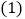 人民大街总长不小于________千米;
人民大街总长不小于________千米; 将最后一名乘客送往目的地时,小李距离下午出车时的出发点多远?
将最后一名乘客送往目的地时,小李距离下午出车时的出发点多远?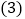 若出租车耗油量为每千米
若出租车耗油量为每千米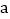 升,这天下午小李共耗油多少升?
升,这天下午小李共耗油多少升? -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,以AB为斜边,作直角△ABD,使点D落在△ABC内,∠ADB=90°.
(1)如图1,若AB=AC,∠DBA=60°,AD=7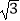 ,点P、M分别为BC、AB边的中点,连接PM,求线段PM的长;
,点P、M分别为BC、AB边的中点,连接PM,求线段PM的长;
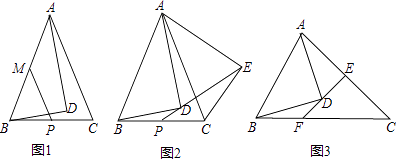
(2)如图2,若AB=AC,把△ABD绕点A逆时针旋转一定角度,得到△ACE,连接ED并延长交BC于点P,求证:BP=CP;
(3)如图3,若AD=BD,过点D的直线交AC于点E,交BC于点F,EF⊥AC,且AE=EC,请直接写出线段BF、FC、AD之间的关系(不需要证明).
相关试题

