搜索
【题目】P为正整数，现规定P!PP1P2…21，若m!120，则正整数m_________．
参考答案：
【答案】5
【解析】
根据规定P!是从1开始连续P个整数的积，即可得到1×2×3×4×…×（m-1）m=120，再由1×2×3×4×5=120，可得正整数m的值．
解：∵P!=P（P-1）（P-2）…×2×1=1×2×3×4×…×（p-2）（p-1），
∴m!=1×2×3×4×…×（m-1）m=120，
∵1×2×3×4×5=120，
∴m=5．
故答案为：5．
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算：
①3+4×（﹣2）；
②1﹣（2﹣3）2×（﹣2）3；
③|﹣9|÷3+（
﹣
）×12+32；④2﹣[1﹣（1﹣0.5×
）]×[2﹣（﹣3）2]﹣22 -
科目： 来源： 题型：
查看答案和解析>>【题目】绝对值小于3.5的整数的个数是( ).
A. 8 B. 7 C. 6 D. 5
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，一次函数的图象与反比例函数的图象交于第二、四象限内的A，B两点，与x轴交于点C，与y轴交于点D，点B的坐标是（m，﹣4），连接AO，AO=5，sin∠AOC=
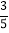．（1）求反比例函数的解析式；
（2）连接OB，求△AOB的面积．
-
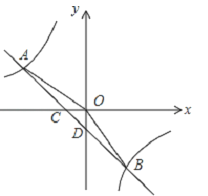
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知抛物线y=x2+bx+c经过A（-1，0）、B（3，0）两点，点C是抛物线与y轴的交点．
（1）求抛物线的解析式和顶点坐标；
（2）当0＜x＜3时，求y的取值范围；
（3）在抛物线的对称轴上是否存在点M，使△BCM是等腰三角形，若存在请直接写出点M坐标，若不存在请说明理由．
-
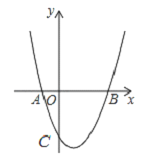
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一楼房AB后有一假山，山坡斜面CD与水平面夹角为30°，坡面上点E处有一亭子，测得假山坡脚C与楼房水平距离BC=10米，与亭子距离CE=20米，小丽从楼房顶测得点E的俯角为45°．求楼房AB的高（结果保留根号）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，将两个完全相同的三角形纸片ABC和DEC重合放置，其中∠C=90°，∠B=∠E=30°.
（1）操作发现
如图2，固定△ABC，使△DEC绕点C旋转，当点D恰好落在AB边上时，填空：
①线段DE与AC的位置关系是_________；
②设△BDC的面积为S1，△AEC的面积为S2，则S1与S2的数量关系是____________.
（2）猜想论证
当△DEC绕点C旋转到图3所示的位置时，小明猜想（1）中S1与S2的数量关系仍然成立，并尝试分别作出了△BDC和△AEC中BC、CE边上的高，请你证明小明的猜想.
（3）拓展探究
已知∠ABC=60°，点D是其角平分线上一点，BD=CD=4，DE//AB交BC于点E（如图4）.若在射线BA上存在点F，使
，请直接写出相应的BF的长.
相关试题
