【题目】已知数轴上两点![]() 所表示的数分别为
所表示的数分别为![]() 和
和![]() ,且满足
,且满足![]() ,
,![]() 为原点.
为原点.
(1)试求![]() 和
和![]() 的值;
的值;
(2)点![]() 从
从![]() 点出发向右运动,经过3秒后点
点出发向右运动,经过3秒后点![]() 到
到![]() 点的距离是点
点的距离是点![]() 到
到![]() 点距离的3倍,求点
点距离的3倍,求点![]() 的运动速度?
的运动速度?
(3)点![]() 以一个单位每秒的速度从点
以一个单位每秒的速度从点![]() 向右运动,同时点
向右运动,同时点![]() 从点
从点![]() 出发以5个单位每秒的速度向左运动,点
出发以5个单位每秒的速度向左运动,点![]() 从点
从点![]() 出发,以20个单位每秒的速度向右运动.在运动过程中,
出发,以20个单位每秒的速度向右运动.在运动过程中,![]() 分别为
分别为![]() 的中点,问
的中点,问![]() 的值是否发生变化,请说明理由.
的值是否发生变化,请说明理由.
参考答案:
【答案】(1)![]() ;(2)2个单位/秒或5个单位/秒;(3)
;(2)2个单位/秒或5个单位/秒;(3)![]() 的值不发生变化,其值为2,理由见解析.
的值不发生变化,其值为2,理由见解析.
【解析】
(1)利用非负数的性质求解;
(2)设点![]() 运动的速度为v个单位/秒,则3s后点
运动的速度为v个单位/秒,则3s后点![]() 表示的数为3v,AC=3v+3,再分点C在点B的左侧或右侧两种情况,列方程即可求解;
表示的数为3v,AC=3v+3,再分点C在点B的左侧或右侧两种情况,列方程即可求解;
(3)设运动的时间为![]() ,根据题意用t表示出PQ,OD,MN的长,进而求出答案.
,根据题意用t表示出PQ,OD,MN的长,进而求出答案.
解:(1)∵|a+3|+(b-9)2020=0,
∴a+3=0且b-9=0,
∴a=-3,b=9;
(2)设点![]() 运动的速度为v个单位/秒,则3s后点
运动的速度为v个单位/秒,则3s后点![]() 表示的数为3v,
表示的数为3v,
又由(1)知,点A表示的数为-3,点B表示的数为9,
∴![]() ,
,
当点C在点B左侧时,BC=9-3v,则![]() ,解得v=2;
,解得v=2;
当点C在点B右侧时,BC=3v-9,则![]() ,解得v=5,
,解得v=5,
故点C的运动速度为2个单位/秒或5个单位/秒;
(3)![]() 的值不发生变化,理由如下:
的值不发生变化,理由如下:
设运动的时间为![]() ,则
,则![]() 表示的数为
表示的数为![]() ,
,![]() 表示的数为
表示的数为![]() ,
,![]() 表示的数为
表示的数为![]() ,
,
又![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,
的中点,
∴![]() 表示的数为
表示的数为![]() ,
,![]() 表示的数为
表示的数为![]() ,
,
∴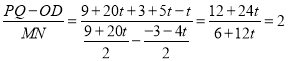 .
.
即![]() 的值不发生变化,其值为2.
的值不发生变化,其值为2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,以等边△ABC的边BC为直径作⊙O,分别交AB,AC于点D,E,过点D作DF⊥AC交AC于点F.
(1)求证:DF是⊙O的切线;
(2)若等边△ABC的边长为8,求由
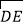 、DF、EF围成的阴影部分面积.
、DF、EF围成的阴影部分面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形AOBC中,OB=4,OA=3.分别以OB,OA所在直线为x轴,y轴,建立如图1所示的平面直角坐标系.F是BC边上一个动点(不与B,C重合),过点F的反比例函数y=
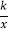 (k>0)的图象与边AC交于点E.
(k>0)的图象与边AC交于点E.(1)当点F运动到边BC的中点时,求点E的坐标;
(2)连接EF,求∠EFC的正切值;
(3)如图2,将△CEF沿EF折叠,点C恰好落在边OB上的点G处,求此时反比例函数的解析式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】出租车司机小傅某天下午营运全是在东西走向的大道上行驶的.若如果规定向东为正,则行车里程(单位:km)如下:
+11,-2,+3,+10,-11,+5,-15,-8
(1)当把最后一名乘客送到目的地时,小傅距离出车地点的距离为多少?
(2)若每千米的营运额为7元,成本为1.5元/km,则这天下午他盈利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若规定
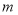 ,
,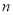 两数之间满足一种运算。 记作
两数之间满足一种运算。 记作 ,若
,若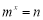 ,则
,则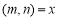 .我们叫这样的数对称为“一青一对”。例如:因为
.我们叫这样的数对称为“一青一对”。例如:因为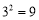 .所以
.所以
(1)根据上述规定要求,请完成填空:
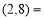 ________.
________. 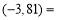 ________.
________. 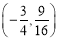 __________
__________(2)计算
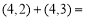 (___________)并写出计算过程
(___________)并写出计算过程(3)在正整数指数幂的范围内,若
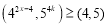 恒成立, 且
恒成立, 且 只有两个正整数解,求
只有两个正整数解,求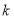 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在平面直角坐标系中,点
 的坐标是
的坐标是 ,点
,点 是第一象限内一动点。
是第一象限内一动点。(1) ①:如图①.若动点
 满足
满足 ,且
,且 ,求点
,求点 的坐标。
的坐标。②:如图②,在第(1)问的条件下,将
 逆时针旋转至如图
逆时针旋转至如图 所示位置,求
所示位置,求 的值.
的值.(2)如图③,若点
 与点
与点 关于轴对称,且
关于轴对称,且 , 若动点
, 若动点 满足
满足 ',问:
',问: 的值是否发生变化?若变化,请说明理由,若不变化,请求出其值。
的值是否发生变化?若变化,请说明理由,若不变化,请求出其值。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D.

(1)求证:△ADC≌△CEB.
(2)AD=5cm,DE=3cm,求BE的长度.
相关试题

