【题目】已知一个一次函数的图象与一个反比例函数的图象交于点P(﹣2,1)、Q(1,m).
(1)分别求出这两个函数的表达式.
(2)在同一平面直角坐标系中画出这两个函数的图象,根据图象回答,当x取何值时,一次函数的值大于反比例函数的值?
参考答案:
【答案】(1)一次函数的解析式为y=﹣x﹣1;(2)当0<x<1或x<﹣2时一次函数的值大于反比例函数的值.见解析
【解析】
试题分析:(1)设出反比例函数关系式,利用代定系数法把P(﹣2,1)代入函数解析式即可.由于Q点也在反比例函数图象上,所以把Q点坐标代入反比例函数解析式中即可得到Q点坐标,求出m的值,利用待定系数法求一次函数解析式;
(2)根据图象可得到答案,注意反比例函数图象与y轴无交点,所以分开看.
解:(1)设反比例函数的解析式为y=![]()
∵反比例函数经过点P(﹣2,1),
∴a=﹣2×1,
∴a=﹣2,
∴反比例函数的解析式为y=﹣![]() ,
,
∵Q(1,m)在反比例函数图象上,
∴m=﹣2,
设一次函数的解析式为y=kx+b
∵P(﹣2,1),Q(1,﹣2)在一次函数图象上
∴![]() ,
,
∴![]() ,
,
∴一次函数的解析式为y=﹣x﹣1;
(2)如图所示:
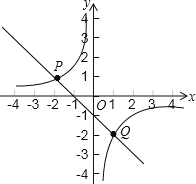
由图可知:当0<x<1或x<﹣2时一次函数的值大于反比例函数的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有两个十分喜欢探究的同学小明和小芳,他们善于将所做的题目进行归类,下面是他们的探究过程。
(1)解题与归纳
①小明摘选了以下各题,请你帮他完成填空。
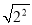 = ;
= ; 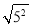 = ;
= ; 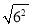 = ;
= ; 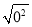 = ;
= ; 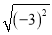 = ;
= ; 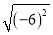 = ;
= ; ②归纳:对于任意数a,有
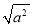 =
= ③小芳摘选了以下各题,请你帮她完成填空。
 = ;
= ; 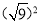 = ;
= ; 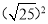 = ;
= ; 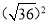 = ;
= ; 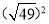 = ;
= ; 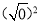 = ;
= ; ④归纳:对于任意非负数a,有
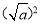 =
= (2)应用
根据他们归纳得出的结论,解答问题。
数a,b在数轴上的位置如图所示,化简:
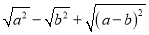 -
-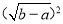

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两辆汽车同时分别从A、B两城沿同一条高速公路匀速驶向C城.已知A、C两城的距离为360km,B、C两城的距离为320km,甲车比乙车的速度快10km/h,结果两辆车同时到达C城.设乙车的速度为xkm/h.
(1)根据题意填写下表:
行驶的路程(km)
速度(km/h)
所需时间(h)
甲车
360
乙车
320
x
(2)求甲、乙两车的速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市荸荠喜获丰收,某生产基地收获荸荠40吨.经市场调查,可采用批发、零售、加工销售三种销售方式,这三种销售方式每吨荸荠的利润如下表:
销售方式 批发 零售 加工销售
利润(百元/吨) 12 22 30
设按计划全部售出后的总利润为y百元,其中批发量为x吨,且加工销售量为15吨.
(1)求y与x之间的函数关系式;
(2)若零售量不超过批发量的4倍,求该生产基地按计划全部售完荸荠后获得的最大利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交BC于点G,连接AG,则BG= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知菱形ABCD的两条对角线分别为6和8,M、N分别是边BC、CD的中点,P是对角线BD上一点,则PM+PN的最小值= .
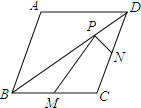
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D是BC的中点,点E,F分别在线段AD及其延长线上,且DE=DF.给出下列条件:
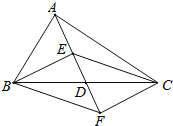
①BE⊥EC;②BF∥CE;③AB=AC;
从中选择一个条件使四边形BECF是菱形,你认为这个条件是 (只填写序号).
相关试题

