【题目】如图(1),在![]() 中,已知
中,已知![]() ,
,![]() ,把一块含
,把一块含![]() 角的三角板
角的三角板![]() 的直角顶点
的直角顶点![]() 放在
放在![]() 的中点上(直角三角板的短直角边为
的中点上(直角三角板的短直角边为![]() ,长直角边为
,长直角边为![]() ),将直角三角板
),将直角三角板![]() 绕
绕![]() 点按逆时针方向旋转.
点按逆时针方向旋转.
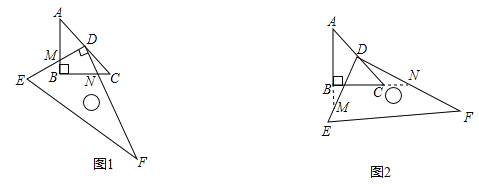
(1)在图(1)中,![]() 交
交![]() 于
于![]() ,
,![]() 交
交![]() 于
于![]() .
.
①证明![]() ;
;
②在这一过程中,直角三角板![]() 与
与![]() 的重叠部分为四边形
的重叠部分为四边形![]() ,请说明四边形
,请说明四边形![]() 的面积是否发生变化?若发生变化,请说明是如何变化的,若不发生变化,求出其面积.
的面积是否发生变化?若发生变化,请说明是如何变化的,若不发生变化,求出其面积.
(2)继续旋转至如图(2)的位置,延长![]() 交
交![]() 于
于![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,
,![]() 是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
参考答案:
【答案】(1)①见解析;②四边形![]() 的面积不发生变化.
的面积不发生变化.![]() ;(2)
;(2)![]() 仍然成立.证明见解析;(3)
仍然成立.证明见解析;(3)![]() .
.
【解析】
(1)①连接BD,证明△DMB≌△DNC.根据已知,全等条件已具备两个,再证出∠MDB=∠NDC,用ASA证明全等,
②四边形DMBN的面积不发生变化,因为它的面积始终等于△ABC面积的一半;
(2)成立.同样利用(1)中的证明方法可以证出△DMB≌△DNC;
(1)①如图1,连接DB,在Rt△ABC中,AB=BC,AD=DC,
∴DB=DC=AD,∠BDC=90°,
∴∠ABD=∠C=45°,
∵∠MDB+∠BDN=∠CDN+∠BDN=90°,
∴∠MDB=∠NDC,
∴△BMD≌△CND(ASA),
∴DM=DN;
②四边形DMBN的面积不发生变化;
由①知△BMD≌△CND,
∴S△BMD=S△CND,
∴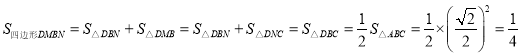 .
.
(2)![]() 仍然成立.证明:
仍然成立.证明:
如图(2),联结![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
在![]() 和
和![]() 中,
中,
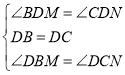 ,
,
∴![]() ≌
≌![]() (ASA).
(ASA).
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】近年来,地震、泥石流等自然灾害频繁发生,造成极大的生命和财产损失.为了更好地做好“防震减灾”工作,我市相关部门对某中学学生“防震减灾”的知晓率采取随机抽样的方法进行问卷调查,调查结果分为“非常了解”、“比较了解”、“基本了解”和“不了解”四个等级.小明根据调查结果绘制了如图1、2的统计图,请根据提供的信息回答问题:
(1)本次调查中,样本容量是________;
(2)扇形统计图中“基本了解”部分所对应的扇形圆心角是________;在该校2000名学生中随机提问一名学生,对“防震减灾”不了解的概率的估计值为________;
(3)请在图2中补全频数分布直方图.

图1 图2
-
科目: 来源: 题型:
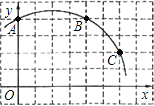
查看答案和解析>>【题目】如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:
(1)在图中确定该圆弧所在圆的圆心D点的位置,并写出点D点坐标为________.
(2)连接AD、CD,求⊙D的半径及
 的长;
的长;(3)有一点E(6,0),判断点E与⊙D的位置关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,将直角三角形的直角顶点放在点
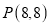 处,两直角边与坐标轴交于如图所示的点
处,两直角边与坐标轴交于如图所示的点 和点
和点 ,则
,则 的值为______.
的值为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣x+2与反比例函数y=
 (k≠0)的图象交于A(a,3),B(3,b)两点,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D.
(k≠0)的图象交于A(a,3),B(3,b)两点,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D.(1)求a,b的值及反比例函数的解析式;
(2)若点P在直线y=﹣x+2上,且S△ACP=S△BDP,请求出此时点P的坐标;
(3)在x轴正半轴上是否存在点M,使得△MAB为等腰三角形?若存在,请直接写出M点的坐标;若不存在,说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)某工厂生产一种产品,当产量至少为10吨,但不超过55吨时,每吨的成本
 (万元/吨)与产量
(万元/吨)与产量 (吨)之间是一次函数关系,函数
(吨)之间是一次函数关系,函数 与自变量
与自变量 的部分对应值如下表:
的部分对应值如下表: (吨)
(吨)10
20
30
 (万元/吨)
(万元/吨)45
40
35
(1)求
 与
与 的函数关系式,并写出自变量
的函数关系式,并写出自变量 的取值范围;
的取值范围;(2)当投入生产这种产品的总成本为1200万元时,求该产品的总产量;(注:总成本=每吨成本×总产量)
(3)市场调查发现,这种产品每月销售量
 (吨)与销售单价
(吨)与销售单价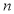 (万元/吨)之间满足如图所示的函数关系.该厂第一个月按同一销售单价卖出这种产品25吨,请求出该厂第一个月销售这种产品获得的利润.(注:利润=售价—成本)
(万元/吨)之间满足如图所示的函数关系.该厂第一个月按同一销售单价卖出这种产品25吨,请求出该厂第一个月销售这种产品获得的利润.(注:利润=售价—成本)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:∠MAN=60°,点B在射线AM上,AB=4(如图).P为直线AN上一动点,以BP为边作等边三角形BPQ(点B,P,Q按顺时针排列),O是△BPQ的外心.
(1)当点P在射线AN上运动时,求证:点O在∠MAN的平分线上;



(2)当点P在射线AN上运动(点P与点A不重合)时,AO与BP交于点C,设AP=x,AC﹒AO=y,求y关于x的函数解析式,并写出自变量的取值范围;
(3)若点D在射线AN上,AD=2,圆I为△ABD的内切圆.当△BPQ的边BP或BQ与圆I相切时,请直接写出点A与点O的距离.
相关试题

