【题目】已知:∠MAN=60°,点B在射线AM上,AB=4(如图).P为直线AN上一动点,以BP为边作等边三角形BPQ(点B,P,Q按顺时针排列),O是△BPQ的外心.
(1)当点P在射线AN上运动时,求证:点O在∠MAN的平分线上;



(2)当点P在射线AN上运动(点P与点A不重合)时,AO与BP交于点C,设AP=x,AC﹒AO=y,求y关于x的函数解析式,并写出自变量的取值范围;
(3)若点D在射线AN上,AD=2,圆I为△ABD的内切圆.当△BPQ的边BP或BQ与圆I相切时,请直接写出点A与点O的距离.
参考答案:
【答案】 (1)详见解析;(2)y=4x,其中自变量的取值范围为x>0;(3))①当BP与圆I相切时,AO=![]() ;②当BP与圆I相切时,AO=
;②当BP与圆I相切时,AO=![]() ;③当BQ与圆I相切时,AO=0.
;③当BQ与圆I相切时,AO=0.
【解析】
(1)证O在∠MAN的平分线上,可证O到角两边的距离相等,分两种情况:①OB不与AM垂直,过O作OT⊥AN,OH⊥AM,可通过构建全等三角形来求解.连接OB,OP,则OB=OP,只需证明△OHB与△OTP全等即可.这两个三角形中,已知的条件有OB=OP,一组直角.只需再证得一组角对应相等即可,∠HOT和∠BOP都等于120°,因此∠BOH=∠TOP,则两三角形全等,OT=OH.由此得证;②当OB⊥AM时,由于OB=OP,只需证明OP⊥AN即可.由于∠BOP=120°,而∠ABO=90°,∠MAN=60°,根据四边形的内角和为360°,即可求得OP⊥AN,由此可得证;
(2)本题要通过相似三角形ACP和ABO来求解.这两个三角形中,已知了∠BAO=∠CAP(在1题中已经证得),只需再找出一组对应角相等即可,在△ACP和△OBC中,∠CAP=∠OBC=30°,∠ACP=∠BCO,因此∠APC=∠AOB,由此证得两三角形相似,可得出关于AB,AC,AO,AP的比例关系式,据此可求出y,x的函数关系式;
(3)本题分三种情况:
①圆I在△BPQ外,且与BP边相切,此时D、P重合,AD=AP=2,AB=4,∠MAN=60°,因此△ABP为直角三角形,不难得出△ABO也是直角三角形,因此可得出△ABO≌△APB,AO=BP=2![]() ;②圆I在△BPQ内,与BP,PQ边相切时,此时P与A重合,可在直角三角形ODA中,根据AD=2,∠DAO=30°,求得AO=
;②圆I在△BPQ内,与BP,PQ边相切时,此时P与A重合,可在直角三角形ODA中,根据AD=2,∠DAO=30°,求得AO=![]() ;③圆I在△BPQ内,与BQ边相切时,A,O重合,因此AO=0.
;③圆I在△BPQ内,与BQ边相切时,A,O重合,因此AO=0.
(1)证明:如图1,连接OB,OP.
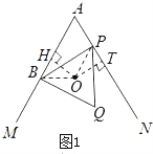
∵O是等边三角形BPQ的外心,∴圆心角∠BOP=![]() =120°.
=120°.
当∠MAN=60°,不垂直于AM时,作OT⊥AN,则OB=OP.
由∠HOT+∠A+∠AHO+∠ATO=360°,且∠A=60°,∠AHO=∠ATO=90°,
∴∠HOT=120°,
∴∠BOH=∠POT,
∴Rt△BOH≌Rt△POT.
∴OH=OT,
∴点O在∠MAN的平分线上;
(2)如图2,
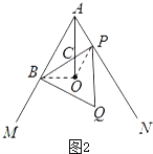
∵AO平分∠MAN,且∠MAN=60°,
∴∠BAO=∠PAO=30°,
由(1)知,OB=OP,∠BOP=120°,
∴∠CBO=30°,
∴∠CBO=∠PAC,
∵∠BCO=∠PCA,
∴∠AOB=∠APC,
∴△ABO∽△ACP,
∴![]() ,
,
∴AC﹒AO=AB﹒AP,
∴y=4x,其中自变量的取值范围为:x>0;
(3)①如图3,当BP与圆I相切时,AO=![]() ;
;
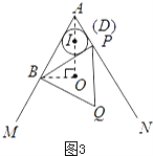
②如图4,当BP与圆I相切时,AO=![]() ;
;
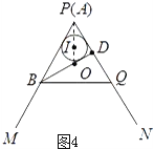
③如图5,
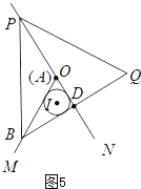
当BQ与圆I相切时,AO=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),在
 中,已知
中,已知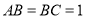 ,
,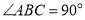 ,把一块含
,把一块含 角的三角板
角的三角板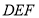 的直角顶点
的直角顶点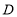 放在
放在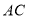 的中点上(直角三角板的短直角边为
的中点上(直角三角板的短直角边为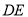 ,长直角边为
,长直角边为 ),将直角三角板
),将直角三角板 绕
绕 点按逆时针方向旋转.
点按逆时针方向旋转.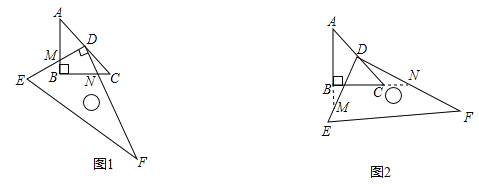
(1)在图(1)中,
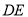 交
交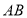 于
于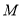 ,
, 交
交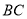 于
于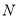 .
.①证明
 ;
;②在这一过程中,直角三角板
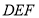 与
与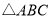 的重叠部分为四边形
的重叠部分为四边形 ,请说明四边形
,请说明四边形 的面积是否发生变化?若发生变化,请说明是如何变化的,若不发生变化,求出其面积.
的面积是否发生变化?若发生变化,请说明是如何变化的,若不发生变化,求出其面积.(2)继续旋转至如图(2)的位置,延长
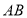 交
交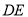 于
于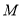 ,延长
,延长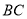 交
交 于
于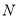 ,
, 是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
是否仍然成立?若成立,请给出证明;若不成立,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣x+2与反比例函数y=
 (k≠0)的图象交于A(a,3),B(3,b)两点,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D.
(k≠0)的图象交于A(a,3),B(3,b)两点,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D.(1)求a,b的值及反比例函数的解析式;
(2)若点P在直线y=﹣x+2上,且S△ACP=S△BDP,请求出此时点P的坐标;
(3)在x轴正半轴上是否存在点M,使得△MAB为等腰三角形?若存在,请直接写出M点的坐标;若不存在,说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)某工厂生产一种产品,当产量至少为10吨,但不超过55吨时,每吨的成本
 (万元/吨)与产量
(万元/吨)与产量 (吨)之间是一次函数关系,函数
(吨)之间是一次函数关系,函数 与自变量
与自变量 的部分对应值如下表:
的部分对应值如下表: (吨)
(吨)10
20
30
 (万元/吨)
(万元/吨)45
40
35
(1)求
 与
与 的函数关系式,并写出自变量
的函数关系式,并写出自变量 的取值范围;
的取值范围;(2)当投入生产这种产品的总成本为1200万元时,求该产品的总产量;(注:总成本=每吨成本×总产量)
(3)市场调查发现,这种产品每月销售量
 (吨)与销售单价
(吨)与销售单价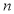 (万元/吨)之间满足如图所示的函数关系.该厂第一个月按同一销售单价卖出这种产品25吨,请求出该厂第一个月销售这种产品获得的利润.(注:利润=售价—成本)
(万元/吨)之间满足如图所示的函数关系.该厂第一个月按同一销售单价卖出这种产品25吨,请求出该厂第一个月销售这种产品获得的利润.(注:利润=售价—成本)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形ABCD中,AB=4,AD=m,动点P从点D出发,在边DA上以每秒1个单位的速度向点A运动,连接CP,作点D关于直线PC的对称点E,设点P的运动时间为t(s).
(1)若m=6,求当P,E,B三点在同一直线上时对应的t的值.
(2)已知m满足:在动点P从点D到点A的整个运动过程中,有且只有一个时刻t,使点E到直线BC的距离等于3,求所有这样的m的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图, AF平分∠BAC,BC⊥AF, 垂足为E,点D与点A关于点E对称,PB分别与线段CF,AF相交于P,M.

(1)求证:AB=CD;
(2)若∠BAC=2∠MPC,请你判断∠F与∠MCD的数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
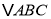 中,
中,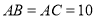 厘米,
厘米, 厘米,点
厘米,点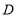 为
为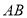 的中点.
的中点.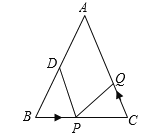
(1)如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1秒后,
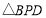 与
与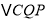 是否全等,请说明理由;
是否全等,请说明理由;②若点Q的运动速度与点P的运动速度不相等,
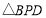 与
与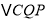 是否可能全等?若能,求出全等时点Q的运动速度和时间;若不能,请说明理由.
是否可能全等?若能,求出全等时点Q的运动速度和时间;若不能,请说明理由.(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿
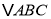 三边运动,求经过多长时间点P与点Q第一次在
三边运动,求经过多长时间点P与点Q第一次在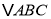 的哪条边上相遇?
的哪条边上相遇?
相关试题

