Question

【题目】如图，在正方形ABCD中，AB＝4，E为BC上一点，F为CD上一点，且AE＝AF.设△AEF的面积为y，CE＝x.

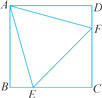
(第11题)

(1)求y关于x的函数表达式．

(2)当△AEF为正三角形时，求△AEF的面积．

Answer 1

【答案】(1). y＝－x2＋4x. (2). 32－48.

【解析】试题分析：（1）根据AB，CE长度，利用S△AEF=16-S△ABE-S△ADF-S△CE即可解决．
（2）根据△AEF为正三角形时得∠BAE=15°，在AB上取一点M使得AM=ME，则∠MAE=∠AEM=15°，所以∠BME=30°，设BE=a，则AM=ME=2a，BM=4-2xa，在RT△MBE利用勾股定理即可求出a，进而得出EC，再利用（1）结论计算．

试题解析：

(1)∵四边形ABCD为正方形，

∴∠B＝∠D＝90°，AB＝AD.

又∵AE＝AF，∴Rt△ABE≌Rt△ADF(HL)．

∴BE＝DF.∴CE＝CF.

∵CE＝x，AB＝4，∴CF＝x，BE＝DF＝4－x，

∴S△ADF＝S△ABE＝AB·BE＝×4×(4－x)＝8－2x，S△CEF＝CE·CF＝x2，

∴y＝S正方形ABCD－2S△ABE－S△CEF＝42－2(8－2x)－x2＝－x2＋4x.

(2)当△AEF为正三角形时，AE＝EF，

∴AE2＝EF2，即16＋(4－x)2＝2x2.

整理，得x2＋8x－32＝0，解得x＝－4±4.

又∵x>0，∴x＝4－4.

∴y＝－x2＋4x＝－×(4－4)2＋4×(4－4)＝32－48，即S△AEF＝32－48.

∴当△AEF为正三角形时，△AEF的面积为32－48.