【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC,AC分别交于D,E两点,过点D作DH⊥AC于点H. 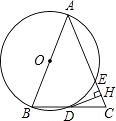
(1)判断DH与⊙O的位置关系,并说明理由;
(2)求证:H为CE的中点;
(3)若BC=10,cosC= ![]() ,求AE的长.
,求AE的长.
参考答案:
【答案】
(1)解:DH与⊙O相切.理由如下:
连结OD、AD,如图,
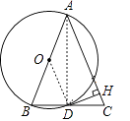
∵AB为直径,
∴∠ADB=90°,即AD⊥BC,
∵AB=AC,
∴BD=CD,
而AO=BO,
∴OD为△ABC的中位线,
∴OD∥AC,
∵DH⊥AC,
∴OD⊥DH,
∴DH为⊙O的切线
(2)证明:连结DE,如图,
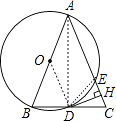
∵四边形ABDE为⊙O的内接四边形,
∴∠DEC=∠B,
∵AB=AC,
∴∠B=∠C,
∴∠DEC=∠C,
∵DH⊥CE,
∴CH=EH,即H为CE的中点
(3)解:在Rt△ADC中,CD= ![]() BC=5,
BC=5,
∵cosC= ![]() =
= ![]() ,
,
∴AC=5 ![]() ,
,
在Rt△CDH中,∵cosC= ![]() =
= ![]() ,
,
∴CH= ![]() ,
,
∴CE=2CH=2 ![]() ,
,
∴AE=AC﹣CE=5 ![]() ﹣2
﹣2 ![]() =3
=3 ![]() .
.
【解析】(1)连结OD、AD,如图,先利用圆周角定理得到∠ADB=90°,则根据等腰三角形的性质得BD=CD,再证明OD为△ABC的中位线得到OD∥AC,加上DH⊥AC,所以OD⊥DH,然后根据切线的判定定理可判断DH为⊙O的切线;(2)连结DE,如图,有圆内接四边形的性质得∠DEC=∠B,再证明∠DEC=∠C,然后根据等腰三角形的性质得到CH=EH;(3)利用余弦的定义,在Rt△ADC中可计算出AC=5 ![]() ,在Rt△CDH中可计算出CH=
,在Rt△CDH中可计算出CH= ![]() ,则CE=2CH=2
,则CE=2CH=2 ![]() , 然后计算AC﹣CE即可得到AE的长.
, 然后计算AC﹣CE即可得到AE的长.
-
科目: 来源: 题型:
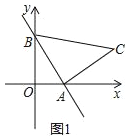
查看答案和解析>>【题目】一次函数y=﹣2x+2的图象与x轴、y轴分别交于点A,B.在y轴左侧有一点P(﹣1,a).
(1)如图1,以线段AB为直角边在第一象限内作等腰Rt△ABC,且∠BAC=90°,求点C的坐标;
(2)当a=
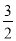 时,求△ABP的面积;
时,求△ABP的面积;(3)当a=﹣2时,点Q是直线y=﹣2x+2上一点,且△POQ的面积为5,求点Q的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】据统计
 两省人口总数基本相同,2001年A省的城镇在校中学生人数为156万,农村在校中学生人数为72万;B省的城镇在校中学生人数为84万,农村在校中学生人数为103万
两省人口总数基本相同,2001年A省的城镇在校中学生人数为156万,农村在校中学生人数为72万;B省的城镇在校中学生人数为84万,农村在校中学生人数为103万 李军同学根据数据画出下面两个复合条形统计图.
李军同学根据数据画出下面两个复合条形统计图.
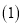 图______ 更好反映两省在校中学生总数;
图______ 更好反映两省在校中学生总数;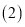 图______ 更好地比较
图______ 更好地比较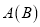 省城镇和农村在校中学生人数;
省城镇和农村在校中学生人数; 说说两种图的特点.
说说两种图的特点. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,一次函数y=﹣ax+b的图象与反比例函数y=
 的图象相交于点A(﹣4,﹣2),B(m,4),与y轴相交于点C.
的图象相交于点A(﹣4,﹣2),B(m,4),与y轴相交于点C. 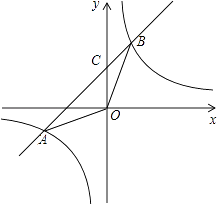
(1)求反比例函数和一次函数的表达式;
(2)求点C的坐标及△AOB的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】我市某化工厂从2008年开始节能减排,控制二氧化硫的排放
 图
图 ,图
,图 分别是该厂
分别是该厂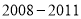 年二氧化硫排放量
年二氧化硫排放量 单位:吨
单位:吨 的两幅不完整的统计图,根据图中信息回答下列问题.
的两幅不完整的统计图,根据图中信息回答下列问题.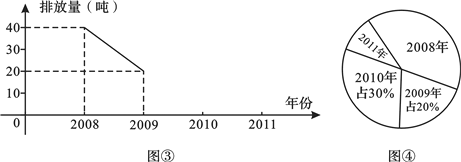
 该厂
该厂 年二氧化硫排放总量是______ 吨;这四年平均每年二氧化硫排放量是______ 吨
年二氧化硫排放总量是______ 吨;这四年平均每年二氧化硫排放量是______ 吨
 把图中折线图补充完整.
把图中折线图补充完整. 年二氧化硫的排放量对应扇形的圆心角是______ 度,2011年二氧化硫的排放量占这四年排放总量的百分比是______ .
年二氧化硫的排放量对应扇形的圆心角是______ 度,2011年二氧化硫的排放量占这四年排放总量的百分比是______ . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,AD为等腰直角△ABC的高,点A和点C分别在正方形DEFG的边DG和DE上,连接BG,AE.
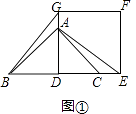
(1)求证:BG=AE;
(2)将正方形DEFG绕点D旋转,当线段EG经过点A时,(如图②所示)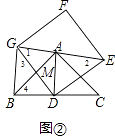
①求证:BG⊥GE;
②设DG与AB交于点M,若AG:AE=3:4,求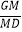 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】.某区在实施居民用水额定管理前,对居民生活用水情况进行了调查,下表是通过简单随机抽样获得的50个家庭去年月平均用水量
 单位:吨
单位:吨 ,并将调查数据进行如下整理:
,并将调查数据进行如下整理:
频数分布表
分组
划记
频数

正正
11


19



合计

2
50
 把上面频数分布表和频数分布直方图补充完整;
把上面频数分布表和频数分布直方图补充完整; 从直方图中你能得到什么信息?
从直方图中你能得到什么信息?  写出两条即可
写出两条即可 ;
; 为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按
为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按 倍价格收费,若要使
倍价格收费,若要使 的家庭收费不受影响,你觉得家庭月均用水量应该定为多少?为什么?
的家庭收费不受影响,你觉得家庭月均用水量应该定为多少?为什么?
相关试题

