【题目】如图①,AD为等腰直角△ABC的高,点A和点C分别在正方形DEFG的边DG和DE上,连接BG,AE.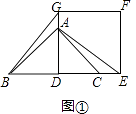
(1)求证:BG=AE;
(2)将正方形DEFG绕点D旋转,当线段EG经过点A时,(如图②所示)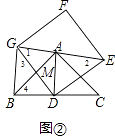
①求证:BG⊥GE;
②设DG与AB交于点M,若AG:AE=3:4,求 ![]() 的值.
的值.
参考答案:
【答案】
(1)
证明:如图①,
∵AD为等腰直角△ABC的高,
∴AD=BD,
∵四边形DEFG为正方形,
∴∠GDE=90°,DG=DE,
在△BDG和△ADE中
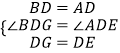 ,
,
∴△BDG≌△ADE,
∴BG=AE
(2)
①证明:如图②,
∵四边形DEFG为正方形,
∴△DEG为等腰直角三角形,
∴∠1=∠2=45°,
由(1)得△BDG≌△ADE,
∴∠3=∠2=45°,
∴∠1+∠3=45°+45°=90°,即∠BGE=90°,
∴BG⊥GE;
②解:设AG=3x,则AE=4x,即GE=7x,
∴DG= ![]() GE=
GE= ![]() x,
x,
∵△BDG≌△ADE,
∴BG=AE=4x,
在Rt△BGA中,AB= ![]() =
= ![]() =5x,
=5x,
∵△ABD为等腰直角三角形,
∴∠4=45°,BD= ![]() AB=
AB= ![]() x,
x,
∴∠3=∠4,
而∠BDM=∠GDB,
∴△DBM∽△DGB,
∴BD:DG=DM:BD,即 ![]() x:
x: ![]() x=DM:
x=DM: ![]() x,解得DM=
x,解得DM= ![]() x,
x,
∴GM=DG﹣DM= ![]() x﹣
x﹣ ![]() x=
x= ![]() x,
x,
∴ ![]() =
= ![]() =
= ![]() .
.
【解析】(1.)如图①,根据等腰直角三角形的性质得AD=BD,再根据正方形的性质得∠GDE=90°,DG=DE,则可根据“SAS“判断△BDG≌△ADE,于是得到BG=AE;
(2.)①如图②,先判断△DEG为等腰直角三角形得到∠1=∠2=45°,再由△BDG≌△ADE得到∠3=∠2=45°,则可得∠BGE=90°,所以BG⊥GE;
②设AG=3x,则AE=4x,即GE=7x,利用等腰直角三角形的性质得DG= ![]() GE=
GE= ![]() x,由(1)的结论得BG=AE=4x,则根据勾股定理得AB=5x,接着由△ABD为等腰直角三角形得到∠4=45°,BD=
x,由(1)的结论得BG=AE=4x,则根据勾股定理得AB=5x,接着由△ABD为等腰直角三角形得到∠4=45°,BD= ![]() AB=
AB= ![]() x,然后证明△DBM∽△DGB,则利用相似比可计算出DM=
x,然后证明△DBM∽△DGB,则利用相似比可计算出DM= ![]() x,所以GM=
x,所以GM= ![]() x,于是可计算出
x,于是可计算出 ![]() 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,一次函数y=﹣ax+b的图象与反比例函数y=
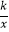 的图象相交于点A(﹣4,﹣2),B(m,4),与y轴相交于点C.
的图象相交于点A(﹣4,﹣2),B(m,4),与y轴相交于点C. 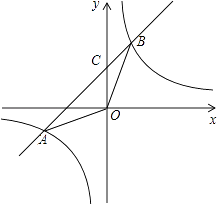
(1)求反比例函数和一次函数的表达式;
(2)求点C的坐标及△AOB的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC,AC分别交于D,E两点,过点D作DH⊥AC于点H.
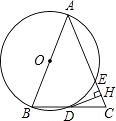
(1)判断DH与⊙O的位置关系,并说明理由;
(2)求证:H为CE的中点;
(3)若BC=10,cosC=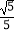 ,求AE的长.
,求AE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】我市某化工厂从2008年开始节能减排,控制二氧化硫的排放
 图
图 ,图
,图 分别是该厂
分别是该厂 年二氧化硫排放量
年二氧化硫排放量 单位:吨
单位:吨 的两幅不完整的统计图,根据图中信息回答下列问题.
的两幅不完整的统计图,根据图中信息回答下列问题.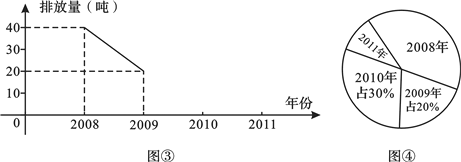
 该厂
该厂 年二氧化硫排放总量是______ 吨;这四年平均每年二氧化硫排放量是______ 吨
年二氧化硫排放总量是______ 吨;这四年平均每年二氧化硫排放量是______ 吨
 把图中折线图补充完整.
把图中折线图补充完整. 年二氧化硫的排放量对应扇形的圆心角是______ 度,2011年二氧化硫的排放量占这四年排放总量的百分比是______ .
年二氧化硫的排放量对应扇形的圆心角是______ 度,2011年二氧化硫的排放量占这四年排放总量的百分比是______ . -
科目: 来源: 题型:
查看答案和解析>>【题目】.某区在实施居民用水额定管理前,对居民生活用水情况进行了调查,下表是通过简单随机抽样获得的50个家庭去年月平均用水量
 单位:吨
单位:吨 ,并将调查数据进行如下整理:
,并将调查数据进行如下整理:
频数分布表
分组
划记
频数

正正
11


19



合计

2
50
 把上面频数分布表和频数分布直方图补充完整;
把上面频数分布表和频数分布直方图补充完整; 从直方图中你能得到什么信息?
从直方图中你能得到什么信息?  写出两条即可
写出两条即可 ;
; 为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按
为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按 倍价格收费,若要使
倍价格收费,若要使 的家庭收费不受影响,你觉得家庭月均用水量应该定为多少?为什么?
的家庭收费不受影响,你觉得家庭月均用水量应该定为多少?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,顶点为M的抛物线y=a(x+1)2﹣4分别与x轴相交于点A,B(点A在点B的右侧),与y轴相交于点C(0,﹣3).

(1)求抛物线的函数表达式;
(2)判断△BCM是否为直角三角形,并说明理由.
(3)抛物线上是否存在点N(点N与点M不重合),使得以点A,B,C,N为顶点的四边形的面积与四边形ABMC的面积相等?若存在,求出点N的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为△ABC外接圆⊙O的直径,点P是线段CA延长线上一点,点E在圆上且满足PE2=PAPC,连接CE,AE,OE,OE交CA于点D.

(1)求证:△PAE∽△PEC;
(2)求证:PE为⊙O的切线;
(3)若∠B=30°,AP= AC,求证:DO=DP.
AC,求证:DO=DP.
相关试题

