【题目】已知BD、CE是△ABC的两条高,直线BD、CE相交于点H.
(1)若∠A=100°,如图,求∠DHE的度数;
(2)若△ABC中∠A=50°,直接写出∠DHE的度数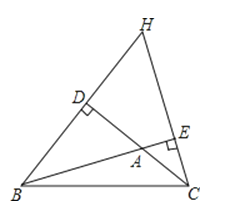
参考答案:
【答案】解:(1)∵BD、CE是△ABC的两条高,
∴∠HDA=∠HEA=90°,
∴∠DHE=180°﹣∠A=80°;
(2)当∠A=50°时,
①△ABC是锐角三角形时,∠DHE=180°﹣50°=130°;
②△ABC是钝角三角形时,∠DHE=∠A=50°;
故答案为:50°或130°.
【解析】(1)根据四边形的内角和是360°,求得∠DHE的度数;
(2)分∠A是锐角时△ABC是锐角三角形,钝角三角形讨论求解即可.
【考点精析】解答此题的关键在于理解三角形的内角和外角的相关知识,掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法错误的是( )
A.一个数同0相乘,仍得0
B.一个数同1相乘,仍得原数
C.一个数同-1相乘,得原数的相反数
D.互为相反数的两数积为1 -
科目: 来源: 题型:
查看答案和解析>>【题目】完成下列推理过程.
如图,DE∥BC,点D、A、E在同一条直线上,
求证:∠BAC+∠B+∠C=180°,
证明:∵DE∥BC
∴∠1=∠B,∠2=∠C
∵D、A、E在同一直线上(已知),
∴∠1+∠BAC+∠2=180°
∴∠BAC+∠B+∠C=180°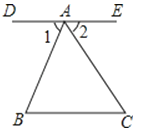
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列调查中,最适合采用普查方式的是( )
A. 调查某班级的每一个同学所穿鞋子的尺码情况
B. 调查某批次烟花爆竹的燃放效果
C. 调查奶茶市场上奶茶的质量情况
D. 调查重庆中学生心里健康现状
-
科目: 来源: 题型:
查看答案和解析>>【题目】五个有理数的积是负数,则五个数中负因数的个数是( )
A.1
B.4
C.5
D.1或3或5 -
科目: 来源: 题型:
查看答案和解析>>【题目】如果将抛物线y=x2+2向右平移1个单位,那么所得新抛物线的表达式是( )
A.y=x2+3
B.y=(x﹣1)2+2
C.y=(x+1)2+2
D.y=x2+1 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知(10x﹣31)(13x﹣17)﹣(13x﹣17)(3x﹣23)可因式分解成(ax+b)(7x+c),其中a、b、c均为整数,求a+b+c的值.
相关试题

