【题目】小英与她的父亲,母亲计划外出旅游,初步选择了延安、西安、汉中、安康四个城市,由于时间仓促,他们只能去其中一个城市,到底去哪一个城市三人意见不统一,在这种情况下,小英父亲建议,用小英学过的摸球游戏来决定,规则如下:
①在一个不透明的袋子中装一个红球(延安)、一个白球(西安)、一个黄球(汉中)和一个黑球(安康),这四个球除颜色的不同外,其余完全相同;
②小英父亲先将袋中球摇匀,让小英从袋中随机摸出一球,父亲记录下其颜色,并将这个球放回袋中摇匀;然后让小英母亲从袋中随机摸出一球,父亲记录下它的颜色;
③若两人所摸出球的颜色相同,则去该球所表示的城市旅游。否则,前面的记录作废,按规则②重新摸球,直到两人所摸出的球的颜色相同为止。
按照上面的规则,请你解答下列问题:
(1)已知小英的理想旅游城市是西安,小英和母亲随机各摸球一次,均摸出白球的概率是多少?
(2)已知小英母亲的理想旅游城市是汉中,小英和母亲随机各摸球一次,至少有一人摸出黄球的概率是多少?
参考答案:
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
试题(1)、首先根据题意画出树状图,然后根据概率的计算法则得出答案;(2)、根据第一题的树状图,得出答案.
试题解析:(1)画树状图得:
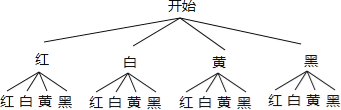
∵共有16种等可能的结果,小明和母亲随机各摸球一次,均摸出白球的只有1种情况,
∴小明和母亲随机各摸球一次,均摸出白球的概率是![]() .
.
(2)、由(1)得:共有16种等可能的结果,小明和母亲随机各摸球一次,至少有一人摸出黄球的有7种情况,
∴小明和母亲随机各摸球一次,至少有一人摸出黄球的概率是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在我们的课本第142页“4.4课题学习”中,有包装纸盒的设计制作方法.这里的右图,是设计师为“XX快递”设计的长方体包装盒的轮廓草图,其中长30CM、宽20CM、高18CM,正面有“快递”字样,上面有“上”字样,棱AB是上盖的掀开处,棱CD是粘合处.请你想想,如何制作这个包装盒,然后完善下面的制作步骤.
步骤1:在符合尺寸规格的硬纸板上,画出这个长方体的展开图(草图).注意,要预留出黏合处,并适当剪去棱角.
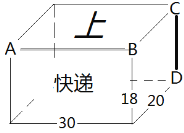
步骤2:在你上面画出的展开草图上,标出对应的A、B、C、D的位置,标出长30CM、宽20CM、高18CM所在线段,并把“上”和“快递”标注在所在面的位置上.
步骤3:裁下展开图,折叠并粘好黏合处,得到长方体包装盒.
-
科目: 来源: 题型:
查看答案和解析>>【题目】让我们一起来探究“边数大于或等于3的多边形的内角和问题”.
规定:连接多边形不相邻的两个顶点的线段叫做多边形的对角线.
尝试:从多边形某一个顶点出发的对角线可以把一个多边形分成若干个三角形,…….这样,就把“多边形内角和问题”转化为“三角形内角和问题”了.……
(1)请你在下面表格中,试一试,做一做,并将表格补充完整:
名称
图形
内角和
三角形

180°
四边形

2
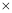 180°=360°
180°=360°五边形

六边形

...
...
……
(2)根据上面的表格,请你猜一猜,七边形的内角和等于 ;…….如果一个多边形有n条边,请你用含有n的代数式表示这个多边形的内角和 .
(3)如果一个多边形的内角和是1260°,请判断这个多边形是几边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD为∠BAC的平分线,添下列条件后,不能证明△ABD≌△ACD的是( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC.填空:∠MON= ;
(2)如图2,∠AOB=90°,∠BOC=x ,仍然分别作∠AOC、∠BOC的平分线OM、ON,能否求出∠MON的度数?若能,求出其值;若不能,说明理由.
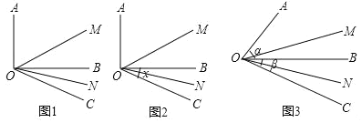
(3)如图3,若∠AOB=α,∠BOC=β(α、β均为锐角,且α>β),仍然分别作∠AOC、∠BOC的平分线OM、ON,能否求出∠MON的度数.若能,求∠MON的度数.
(4)从(1)、(2)、(3)的结果中,你发现了什么规律?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知整数a1,a2,a3,a4,…满足下列条件:a1=0,a2=﹣|a1+1|,a3=﹣|a2+2|,a4=﹣|a3+3|,……以此类推,则a2018的值为( )
A. ﹣1007 B. ﹣1008 C. ﹣1009 D. ﹣2018
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上,点A表示数1,现将点A沿数轴做如下移动:第一次将点A向左移动3个单位长度到达点
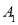 ,第2次将点
,第2次将点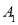 向右平移6个单位长度到达点
向右平移6个单位长度到达点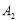 ,第3次将点
,第3次将点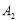 向左移动9个单位长度到达点
向左移动9个单位长度到达点 …,按照这种规律移动下去,则第2017次移动到点
…,按照这种规律移动下去,则第2017次移动到点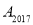 时,
时,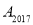 在数轴上对应的实数是_______.
在数轴上对应的实数是_______.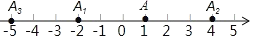
相关试题

