【题目】如图,正方形![]() 的对角线交于点
的对角线交于点![]() 点
点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上(
上(![]() )且
)且![]() ,
,![]() ,
,![]() 的延长线交于点
的延长线交于点![]() ,
,![]() ,
,![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() .
.
(1)求证:![]() .
.
(2)若正方形![]() 的边长为4,
的边长为4,![]() 为
为![]() 的中点,求
的中点,求![]() 的长.
的长.
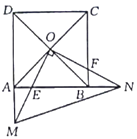
参考答案:
【答案】(1)见解析(2)![]()
【解析】
(1)证△OAM≌△OBN即可得;
(2)作OH⊥AD,由正方形的边长为4且E为OM的中点知OH=HA=2、HM=4,再根据勾股定理得OM=2![]() ,由直角三角形性质知MN=
,由直角三角形性质知MN=![]() OM.
OM.
(1)∵四边形ABCD是正方形,
∴OA=OB,∠DAO=45°,∠OBA=45°,
∴∠OAM=∠OBN=135°,
∵∠EOF=90°,∠AOB=90°,
∴∠AOM=∠BON,
∴△OAM≌△OBN(ASA),
∴OM=ON;
(2)如图,过点O作OH⊥AD于点H,
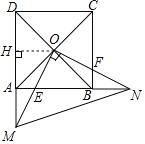
∵正方形的边长为4,
∴OH=HA=2,
∵E为OM的中点,
∴HM=4,
则OM=![]() ,
,
∴MN=![]() OM=2
OM=2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司招聘职员两名,对甲、乙、丙、丁四名候选人进行了笔试和面试,各项成绩满分均为100分,然后再按笔试占60%、面试占40%计算候选人的综合成绩(满分为100分).
他们的各项成绩如下表所示:
修造人
笔试成绩/分
面试成绩/分
甲
90
88
乙
84
92
丙
x
90
丁
88
86
(1)直接写出这四名候选人面试成绩的中位数;
(2)现得知候选人丙的综合成绩为87.6分,求表中x的值;
(3)求出其余三名候选人的综合成绩,并以综合成绩排序确定所要招聘的前两名的人选.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠BAD=130°,∠B=∠D=90°,点E,F分别是线段BC,DC上的动点.当△AEF的周长最小时,则∠EAF的度数为( )

A. 90°B. 80°C. 70°D. 60°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将等边△ABC绕点C顺时针旋转120得到
 EDC,连接AD,BD.
EDC,连接AD,BD.
则下列结论:
①AC=AD;
②BD AC;
AC;
③四边形ACED是菱形.
其中正确的个数是( )
A.O
B.1
C.2
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,∠A=52°,若∠ABC与∠ACB的角平分线交于点D1,得到∠D1,∠ABD1与∠ACD1的角平分线交于点D2,得到∠D2;依此类推,∠ABD4与∠ACD4的角平分线交于点D5,得到∠D5,则∠D5的度数是_____.

-
科目: 来源: 题型:
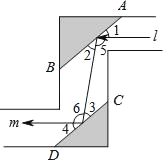
查看答案和解析>>【题目】如图是潜望镜工作原理示意图,阴影部分是平行放置在潜望镜里的两面镜子.已知光线经过镜子反射时,有∠1=∠2,∠3=∠4,请解释进入潜望镜的光线l为什么和离开潜望镜的光线m是平行的?
请把下列解题过程补充完整.
理由:
因为AB∥CD,
根据“ ”,
所以∠2=∠3.
因为∠1=∠2,∠3=∠4,
所以∠1=∠2=∠3=∠4,
所以180°﹣∠1﹣∠2=180°﹣∠3﹣∠4,
即: .
根据“ ”,
所以l∥m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.
(1)若∠A=40°,求∠DBC的度数;
(2)若AE=6,△CBD的周长为20,求BC的长.

相关试题

