【题目】某单位举行“健康人生”徒步走活动,某人从起点体育村沿建设路到市生态园,再沿原路返回,设此人离开起点的路程s(千米)与走步时间t(小时)之间的函数关系如图所示,其中从起点到市生态园的平均速度是4千米/小时,用2小时,根据图像提供信息,解答下列问题. 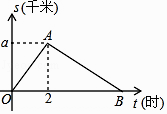
(1)求图中的a值.
(2)若在距离起点5千米处有一个地点C,此人从第一次经过点C到第二次经过点C,所用时间为1.75小时. ①求AB所在直线的函数解析式;
②请你直接回答,此人走完全程所用的时间.
参考答案:
【答案】
(1)解:a=4×2=8
(2)解:①此人返回的速度为(8﹣5)÷(1.75﹣ ![]() )=3(千米/小时),
)=3(千米/小时),
AB所在直线的函数解析式为s=8﹣3(t﹣2)=﹣3t+14.
②当s=﹣3t+14=0时,t= ![]() .
.
答:此人走完全程所用的时间为 ![]() 小时
小时
【解析】(1)根据路程=速度×时间即可求出a值;(2)①根据速度=路程÷时间求出此人返回时的速度,再根据路程=8﹣返回时的速度×时间即可得出AB所在直线的函数解析式;②令①中的函数关系式中s=0,求出t值即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,M,N分别是AD,BC的中点,∠AND=90°,连接CM交DN于点O.
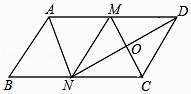
(1)求证:△ABN≌△CDM;
(2)连接MN,求证四边形MNCD是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一艘海警船在A处发现北偏东30°方向相距12海里的B处有一艘可疑货船,该艘货船以每小时10海里的速度向正东航行,海警船立即以每小时14海里的速度追赶,到C处相遇,求海警船用多长时间追上了货船?
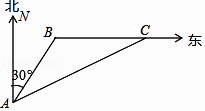
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上点 A、B 到表示-2 的点的距离都为 6,P 为线段 AB 上任一点,C,D 两点分别从 P,B 同时向 A 点移动,且 C 点运动速度为每秒 2 个单位长度,D 点运动速度 为每秒 3 个单位长度,运动时间为 t 秒.
(1)A 点表示数为 ,B 点表示的数为 ,AB= .
(2)若 P 点表示的数是 0,
①运动 1 秒后,求 CD 的长度;
②当 D 在 BP 上运动时,求线段 AC、CD 之间的数量关系式.
(3)若 t=2 秒时,CD=1,请直接写出 P 点表示的数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,以AC为直径作⊙O交BC于点D,交AB于点G,且D是BC的中点,DE⊥AB,垂足为E,交AC的延长线于点F.

(1)求证:直线EF是⊙O的切线;
(2)CF=5,cos∠A= ,求AE的长.
,求AE的长. -
科目: 来源: 题型:
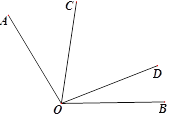
查看答案和解析>>【题目】如图,已知∠AOB=120°,∠COD在∠AOB内部且∠COD=60°,下列说法:
①如果∠AOC=∠BOD,则图中有两对互补的角;
②如果作OE平分∠BOC,则∠AOC=2∠DOE;
③如果作OM平分∠AOC,且∠MON=90°,则ON平分∠BOD;
④如果在∠AOB外部分别作∠AOC、∠BOD的余角∠AOP、∠BOQ,则
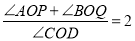 ,
,其中正确的有( )个.
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题8分)如图,在五边形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD.
(1)求证:△ABC≌△AED;
(2)当∠B=140°时,求∠BAE的度数.

相关试题

