【题目】为执行中央“节能减排,美化环境,建设美丽新农村”的国策,我市某村计划建造A、B两种型号的沼气池共20个,以解决该村所有农户的燃料问题.两种型号沼气池的占地面积、使用农户数及造价见下表:
型号 | 占地面积 (单位:m2/个 ) | 使用农户数 (单位:户/个) | 造价 (单位:万元/个) |
A | 15 | 18 | 2 |
B | 20 | 30 | 3 |
已知可供建造沼气池的占地面积不超过365m2,该村农户共有492户.
(1)满足条件的方案共有几种?写出解答过程;
(2)通过计算判断,哪种建造方案最省钱?
参考答案:
【答案】(1)三种;(2)方案三最省钱
【解析】
试题分析:(1)关系式为:A型沼气池占地面积+B型沼气池占地面积≤365;A型沼气池能用的户数+B型沼气池能用的户数≥492;
(2)由(1)得到情况进行分析.
解:(1)设建造A型沼气池x个,则建造B型沼气池(20﹣x)个,
依题意得:![]() ,
,
解得:7≤x≤9.
∵x为整数∴x=7,8,9,
所以满足条件的方案有三种.
(2)
解法①:设建造A型沼气池x个时,总费用为y万元,则:
y=2x+3(20﹣x)=﹣x+60,
∴y随x增大而减小,
当x=9时,y的值最小,此时y=51(万元).
∴此时方案为:建造A型沼气池9个,建造B型沼气池11个.
解法②:由(1)知共有三种方案,其费用分别为:
方案一:建造A型沼气池7个,建造B型沼气池13个,
总费用为:7×2+13×3=53(万元).
方案二:建造A型沼气池8个,建造B型沼气池12个,
总费用为:8×2+12×3=52(万元).
方案三:建造A型沼气池9个,建造B型沼气池11个,
总费用为:9×2+11×3=51(万元).
∴方案三最省钱.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a、b互为相反数,b、c互为倒数,并且m的立方等于它本身.
(1)试求
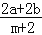 +ac值;
+ac值;(2)若a>1,b<﹣1,且m<0,S=|2a一3b|﹣2|b﹣m|﹣|b+
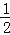 |,试求4(2a一S)+2(2a﹣S)﹣(2a﹣S)的值.
|,试求4(2a一S)+2(2a﹣S)﹣(2a﹣S)的值.(3)若m≠0,当x为有理数时,|x+m|﹣|x﹣m|存在最大值,请求出这个最大值(直接写出答案).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AB为⊙O的直径,点C、D在⊙O上,且BC=6cm,AC=8cm,∠ABD=45°.
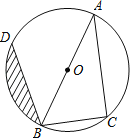
(1)求BD的长;
(2)求图中阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(填空、解答)已知:x1,x2,…x2012都是不等于0的有理数,请你探究以下问题:
(1)若y1=
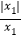 ,则
,则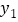 = ;
= ;(2)若y2=
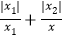 ,则
,则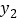 = ;
= ;(3)若y3=
 ,则
,则 = ;
= ;(4)由以上探究可知,y2012=
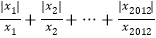 ,
,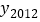 共有 个不同的值。请求出这些不同的y2012的值的绝对值的和。
共有 个不同的值。请求出这些不同的y2012的值的绝对值的和。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知(a+b)2=25,(a﹣b)2=9,则a2+b2的值为_____,ab的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,CD=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.
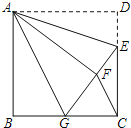
(1)求证:①△ABG≌△AFG; ②求GC的长;
(2)求△FGC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,已知P(a, b)是△ABC的边AC上一点,△ABC经平移后P点的对应点P1(a+3,b-1),则下列平移过程正确的是( )
A. 先向左平移3个单位,再向下平移1个单位 B. 先向右平移3个单位,再向下平移1个单位
C. 先向左平移3个单位,再向上平移1个单位 D. 先向右平移3个单位,再向上平移1个单位
相关试题

