【题目】已知,如图,正方形ABCD的对角线AC,BD相交于点O,正方形A′B′C′D′的顶点A′与点O重合,A′B′交BC于点E,A′D′交CD于点F. 
(1)求证:OE=OF;
(2)若正方形ABCD的对角线长为4,求两个正方形重叠部分的面积为
参考答案:
【答案】
(1)证明:∵正方形ABCD的对角线AC、BD交于点O
∴∠BOC=90°,∠OBC=∠OCD=∠OCF=45°,OB=OC,
∵正方形A'B'C'D'的A'B'交BC于点E,A'D'交CD于点F.
∴∠EOF=90°
∵∠BOE=∠EOF﹣∠EOC=90°﹣∠EOC
∠COF=∠BOC﹣∠EOC=90°﹣∠EOC
∴∠BOE=∠COF.
在△OBE和△OCF中,
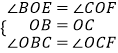 ,
,
∴△BOE≌△COF(ASA).
∴OE=OF
(2)2
【解析】(2)解:∵△BOE≌△COF, ∴S△BOE=S△COF
∴S△EOC+S△COF=S△EOC+S△BOE ,
即S四边形OECF=S△BOC .
∵S△BOC=2,
∴两个正方形重叠部分的面积为2.
故答案为:2.
(1)由正方形的性质可以得出△BOE≌△COF,由全等三角形的性质就可以得出OE=OF;(2)由全等可以得出S△BOE=S△COF , 就可以得出S四边形OECF=S△BOC , S△BOC的面积就可以得出结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】初三年某班共50名学生参加体育测试,全班学生成绩合格率为94%,则不合格的人数有___________人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知am=2,an=3,则an+m=( )
A. 2 B. 3 C. 5 D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据8,3,8,6,7,8,7的众数和中位数分别是( )
A.8,6
B.7,6
C.7,8
D.8,7 -
科目: 来源: 题型:
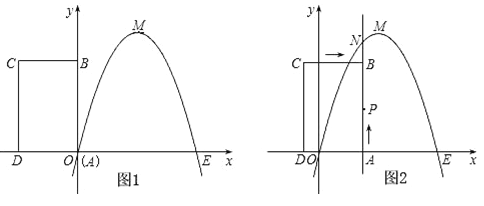
查看答案和解析>>【题目】如图,已知抛物线经过坐标原点O和x轴上另一点E,顶点M的坐标为(2,4);矩形ABCD的顶点A与点O重合,AD、AB分别在x轴、y轴上,且AD=2,AB=3.
(1)求该抛物线所对应的函数关系式;
(2)将矩形ABCD以每秒1个单位长度的速度从如图所示的位置沿x轴的正方向匀速平行移动,同时一动点P也以相同的速度从点A出发向B匀速移动,设它们运动的时间为t秒(0≤t≤3),直线AB与该抛物线的交点为N(如图2所示).
①当t=
 时,判断点P是否在直线ME上,并说明理由;
时,判断点P是否在直线ME上,并说明理由;②设以P、N、C、D为顶点的多边形面积为S,试问S是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出六个多项式:①x2+y2;②﹣x2+y2;③x2+2xy+y2;④x4﹣1;⑤x(x+1)﹣2(x+1);⑥m2﹣mn+
 n2 . 其中,能够分解因式的是(填上序号).
n2 . 其中,能够分解因式的是(填上序号). -
科目: 来源: 题型:
查看答案和解析>>【题目】某品牌的共享自行车企业为了解工作日期间地铁站附近的自行车使用情况,做到精确投放,于星期二当天对荔湾区A、B、C三个地铁站该品牌自行车后使用量进行了统计,绘制如图1和图2所示的统计图,根据图中信息解答下列问题:
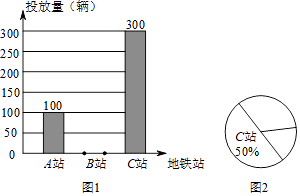
(1)该品牌自行车当天在该三个地铁站区域投放了自行车辆.
(2)请补全图1中的条形统计图;求出地铁A站在图2中所对应的圆心角的度数.
(3)按统计情况,若该品牌车计划在这些区域再投放1200辆,估计在地铁B站应投入多少辆.
相关试题

