【题目】如图(1),在平面直角坐标系中,A(a,0),C(b,2),过C作CB⊥x轴,且满足(a+b)2+ ![]() =0.
=0. 
(1)求三角形ABC的面积.
(2)若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,如图2,求∠AED的度数.
(3)在y轴上是否存在点P,使得三角形ABC和三角形ACP的面积相等?若存在,求出P点坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)解:∵(a+b)2≥0, ![]() ≥0,
≥0,
∴a=﹣b,a﹣b+4=0,
∴a=﹣2,b=2,
∵CB⊥AB
∴A(﹣2,0),B(2,0),C(2,2)
∴三角形ABC的面积= ![]() ×4×2=4
×4×2=4
(2)解:∵CB∥y轴,BD∥AC,
∴∠CAB=∠ABD,
∴∠3+∠4+∠5+∠6=90°,
过E作EF∥AC,
∵BD∥AC,
∴BD∥AC∥EF,
∵AE,DE分别平分∠CAB,∠ODB,
∴∠3=∠4=∠1,∠5=∠6=∠2,
∴∠AED=∠1+∠2= ![]() ×90°=45°
×90°=45°
(3)解:存在.理由如下:
设P点坐标为(0,t),直线AC的解析式为y=kx+b,
把A(﹣2,0)、C(2,2)代入得 ![]() ,
,
解得 ![]() ,
,
∴直线AC的解析式为y= ![]() x+1,
x+1,
∴G点坐标为(0,1),
∴S△PAC=S△APG+S△CPG= ![]() |t﹣1|2+
|t﹣1|2+ ![]() |t﹣1|2=4,解得t=3或﹣1,
|t﹣1|2=4,解得t=3或﹣1,
∴P点坐标为(0,3)或(0,﹣1).

【解析】(1)根据非负数的性质得到a=﹣b,a﹣b+4=0,解得a=﹣2,b=2,则A(﹣2,0),B(2,0),C(2,2),即可计算出三角形ABC的面积=4;(2)由于CB∥y轴,BD∥AC,则∠CAB=∠ABD,即∠3+∠4+∠5+∠6=90°,过E作EF∥AC,则BD∥AC∥EF,然后利用角平分线的定义可得到∠3=∠4=∠1,∠5=∠6=∠2,所以∠AED=∠1+∠2= ![]() ×90°=45°;(3)先根据待定系数法确定直线AC的解析式为y=
×90°=45°;(3)先根据待定系数法确定直线AC的解析式为y= ![]() x+1,则G点坐标为(0,1),然后利用S△PAC=S△APG+S△CPG进行计算.
x+1,则G点坐标为(0,1),然后利用S△PAC=S△APG+S△CPG进行计算.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请写出“等腰三角形的两底角相等”的逆命题:__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列各组数据中,不能作为直角三角形的三边长的是( )
A. 6,8,10 B. 9,12,15
C. 4,5,6 D. 7,24,25
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司投资1200万元购买了一条新生产线生产新产品.根据市场调研,生产每件产品需要成本50元,该产品进入市场后不得低于80元/件且不得超过160元/件,该产品销售量y(万件)与产品售价x(元)之间的关系如图所示.
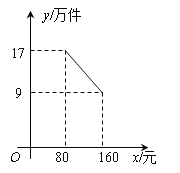
(1)求y与x之间的函数关系式,并写出x的取值范围;
(2)第一年公司是盈利还是亏损?求出当盈利最大或亏损最小时的产品售价;
(3)在(2)的前提下,即在第一年盈利最大或者亏损最小时,公司第二年重新确定产品售价,能否使前两年盈利总额达790万元?若能,求出第二年产品售价;若不能,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,真命题是( )
A. 如果|a|=|b|,那么a=b
B. 三角形的外角一定大于三角形的内角
C. 直角三角形的两个锐角互余
D. 一个角的余角一定小于这个角
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一游客在某城市旅游期间,沿街步行前往著名的电视塔观光,他在A处望塔顶C的仰角为30°,继续前行250m后到达B处,此时望塔顶的仰角为45°.已知这位游客的眼睛到地面的距离约为170cm,假若游客所走路线直达电视塔底.请你计算这座电视塔大约有多高?(结果保留整数.
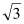 ≈1.7,
≈1.7,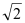 ≈1.4;E,F分别是两次测量时游客眼睛所在的位置.)
≈1.4;E,F分别是两次测量时游客眼睛所在的位置.)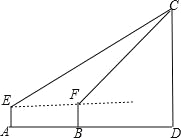
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级共有四个班,各班的人数如图1所示,人数比例如图2所示.
(1)试求出该校八年级的学生总人数;
(2)请补充条形统计表;
(3)在一次数学考试中,1班、2班、3班、4班的平均成绩分别为92分、91分、90分、95分.试求出该校八年级学生在本次数学考试的平均分.

相关试题

