【题目】如图,在Rt△ABC中,∠B=90°,AB=4,BC>AB,点D在BC上,以AC为对角线的平行四边形ADCE中,DE的最小值是 . 
参考答案:
【答案】4
【解析】解:∵四边形ADCE是平行四边形,
∴BC∥AE,
∴当DE⊥BC时,DE最短,
此时∵∠B=90°,
∴AB⊥BC,
∴DE∥AB,
∴四边形ABDE是平行四边形,
∵∠B=90°,
∴四边形ABDE是矩形,
∴DE=AB=4,
∴DE的最小值为4.
所以答案是4.
【考点精析】解答此题的关键在于理解垂线段最短的相关知识,掌握连接直线外一点与直线上各点的所有线段中,垂线段最短;现实生活中开沟引水,牵牛喝水都是“垂线段最短”性质的应用,以及对平行四边形的性质的理解,了解平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A(﹣3,6),B(﹣9,﹣3),以原点O为位似中心,相似比为
 ,把△ABO缩小,则点A的对应点A′的坐标是( )
,把△ABO缩小,则点A的对应点A′的坐标是( )
A.(﹣1,2)
B.(﹣9,18)
C.(﹣9,18)或(9,﹣18)
D.(﹣1,2)或(1,﹣2) -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=10,AC=2
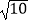 ,BC边上的高AD=6,则另一边BC等于( )
,BC边上的高AD=6,则另一边BC等于( )
A.10
B.8
C.6或10
D.8或10 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:
①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD= .
.
其中正确的结论有( )
A.4个
B.3个
C.2个
D.1个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知折痕AE=5
 cm,且tan∠EFC=
cm,且tan∠EFC=  ,那么矩形ABCD的周长为cm.
,那么矩形ABCD的周长为cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在求1+3+32+33+34+35+36+37+38的值时,张红发现:从第二个加数起每一个加数都是前一个加数的3倍,于是她假设:S=1+3+32+33+34+35+36+37+38①,
然后在①式的两边都乘以3,得:3S=3+32+33+34+35+36+37+38+39②,
②﹣①得,3S﹣S=39﹣1,即2S=39﹣1,
随意S= .
.
得出答案后,爱动脑筋的张红想:如果把“3”换成字母m(m≠0且m≠1),能否求出1+m+m2+m3+m4+…+m2016的值?如能求出,其正确答案是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】
(1)计算:( )﹣1+(π﹣3.14)0﹣2sin60°﹣
)﹣1+(π﹣3.14)0﹣2sin60°﹣  +|1﹣3
+|1﹣3  |;
|;
(2)先化简,再求值:
(a+1﹣ )÷(
)÷(  ),其中a=2+
),其中a=2+  .
.
相关试题

