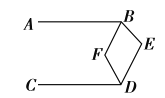
【题目】如下图,![]() ,
,![]() ,
,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
参考答案:
【答案】C
【解析】
首先过点E作EM∥AB,过点F作FN∥AB,由AB∥CD,即可得EM∥AB∥CD∥FN,然后根据两直线平行,同旁内角互补,由∠BED=110°,即可求得∠ABE+∠CDE=250°,又由BF平分∠ABE,DF平分∠CDE,根据角平分线的性质,即可求得∠ABF+∠CDF的度数,又由两直线平行,内错角相等,即可求得∠BFD的度数.
过点E作EM∥AB,过点F作FN∥AB,
∵AB∥CD,
∴EM∥AB∥CD∥FN,
∴∠ABE+∠BEM=180°,∠CDE+∠DEM=180°,
∴∠ABE+∠BED+∠CDE=360°,
∵∠BED=110°,
∴∠ABE+∠CDE=250°,
∵BF平分∠ABE,DF平分∠CDE,
∴∠ABF=![]() ∠ABE,∠CDF=
∠ABE,∠CDF=![]() ∠CDE,
∠CDE,
∴∠ABF+∠CDF=![]() (∠ABE+∠CDE)=125°,
(∠ABE+∠CDE)=125°,
∵∠DFN=∠CDF,∠BFN=∠ABF,
∴∠BFD=∠BFN+∠DFN=∠ABF+∠CDF=125°.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在
 和
和 中
中 ,
, ,
, ,连接
,连接 ,
, ,
, 绕点
绕点 自由旋转.
自由旋转.
(1)当
 在
在 边上时,
边上时,①线段
 和线段
和线段 的关系是____________________;
的关系是____________________;②若
 ,则
,则 的度数为____________;
的度数为____________;(2)如图2,点
 不在
不在 边上,
边上, ,
, 相交于点
相交于点 ,(l)问中的线段
,(l)问中的线段 和线段
和线段 的关系是否仍然成立?并说明理由.
的关系是否仍然成立?并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】快车与慢车分别从甲乙两地同时相向出发,匀速而行,快车到达乙地后停留
 ,然后按原路原速返回,快车与慢车晚
,然后按原路原速返回,快车与慢车晚 到达甲地.快慢两车距各自出发地的路程
到达甲地.快慢两车距各自出发地的路程 与所用的时间
与所用的时间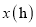 的关系如图所示.
的关系如图所示.
(1)甲乙两地之间的路程为_________________
 ;快车的速度为_________________
;快车的速度为_________________ ;慢车的速度为______________
;慢车的速度为______________ ;
;(2)出发________________
 ,快慢两车距各自出发地的路程相等;
,快慢两车距各自出发地的路程相等;(3)快慢两车出发______________
 相距
相距 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】勾股定理是一个基本的几何定理,早在我国西汉吋期算书《周髀算经》就有“勾三股四弦五”的记载.如果一个直角三角形三边长都是正整数,这样的直角三角形叫“整数直角三角形”;这三个整数叫做一组“勾股数”,如:3,4,5;5,12,13;7,24,25;8,15,17;9,40,41等等都是勾股数.
(1)小李在研究勾股数时发现,某些整数直角三角形的斜边能写成两个整数的平方和,有一条直角边能写成这两个整数的平方差.如3,4,5中,5=22+12,3=22﹣12;5,12,13中,13=32+22,5=32﹣22;请证明:m,n为正整数,且m>n,若有一个直角三角形斜边长为m2+n2,有一条直角长为m2﹣n2,则该直角三角形一定为“整数直角三角形”;
(2)有一个直角三角形两直角边长分别为
 和
和 ,斜边长4
,斜边长4 ,且a和b均为正整数,用含b的代数式表示a,并求出a和b的值;
,且a和b均为正整数,用含b的代数式表示a,并求出a和b的值;(3)若c1=a12+b12,c2=a22+b22,其中,a1、a2、b1、b2均为正整数.证明:存在一个整数直角三角形,其斜边长为c1c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,二氧化碳气体的密度 ρ(kg/m 3)与体积 V(m 3)的反比例函数关系式是
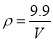 .
. (1)求当 V=5m 3时二氧化碳的密度 ρ;
(2)请写出二氧化碳的密度 ρ随体积 V的增大(或减小)而变化的情况.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如下图,点
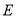 是
是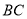 的中点,
的中点,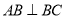 ,
,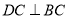 ,
,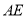 平分
平分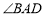 ,下列结论:
,下列结论:①
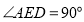 ②
②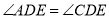 ③
③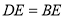 ④
④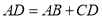
四个结论中成立的是( )
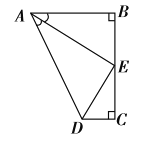
A.①②④B.①②③C.②③④D.①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】一场暴雨过后,一洼地存雨水20米 3,如果将雨水全部排完需 t分钟,排水量为 a米 3/分,且排水时间为5~10分钟
(1)试写出 t与 a的函数关系式,并指出 a的取值范围;
(2)请画出函数图象
(3)根据图象回答:当排水量为3米 3/分时,排水的时间需要多长?
相关试题

