【题目】骰子是6个面上分别写有数字1,2,3,4,5,6的小立方体,它任意两对面上所写的两个数字之和为7.将这样相同的几个骰子按照相接触的两个面上的数字的积为6摆成一个几何体,这个几何体的三视图如图所示.已知图中所标注的是部分面上的数字,则“*”所代表的数是( )
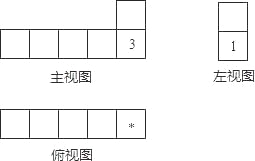
A. 2 B. 4 C. 5 D. 6
参考答案:
【答案】B
【解析】试题解析:利用三视图可以得出,这个几何体有6个小正方体组成,
从正面看,第一层有5个,第二层有一个,并且在最右端,
从主视图上看,最右端,最下面的前面是3,从左视图上看,最左端,最下面的左面是1,
则最右端,最下面的左右分别是1和6,
故最右端下面正方形上下为2,5,利用相接触的两个面上的数字的积为6,
则上面正方形的两个面为下面为3,上面为4,
故所*代表的数为4.
故选B.
-
科目: 来源: 题型:
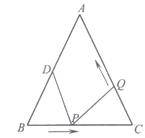
查看答案和解析>>【题目】如图,已知在△ABC中,AB=AC=10cm,BC=8cm,D为AB中点,设点P在线段BC上以3cm/秒的速度由B点向C点运动,点Q在线段CA上由C点向A点运动.
(1)若Q点运动的速度与P点相同,且点P,Q同时出发,经过1秒钟后△BPD与△CQP是否全等,并说明理由;
(2)若点P,Q同时出发,但运动的速度不相同,当Q点的运动速度为多少时,能在运动过程中有△BPD与△CQP全等?
(3)若点Q以(2)中的速度从点C出发,点P以原来的速度从点B同时出发,都是逆时针沿△ABC的三边上运动,经过多少时间点P与点Q第一次在△ABC的哪条边上相遇?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程mx2+(3m+1)x+3=0.
(1)求证:该方程有两个实数根;
(2)如果抛物线y=mx2+(3m+1)x+3与x轴交于A、B两个整数点(点A在点B左侧),且m为正整数,求此抛物线的表达式;
(3)在(2)的条件下,抛物线y=mx2+(3m+1)x+3与y轴交于点C,点B关于y轴的对称点为D,设此抛物线在﹣3≤x≤﹣ 之间的部分为图象G,如果图象G向右平移n(n>0)个单位长度后与直线CD有公共点,求n的取值范围.
之间的部分为图象G,如果图象G向右平移n(n>0)个单位长度后与直线CD有公共点,求n的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】中学生带手机上学的现象越来越受到社会的关注,为此,某记者随机调查了某城区若干名学生家长对这种现象的态度(态度分为:A:无所谓;B:基本赞成;C:赞成;D:反对),并将调查结果绘制成频数折线图1和统计图2(不完整)。请根据图中提供的信息,解答下列问题:
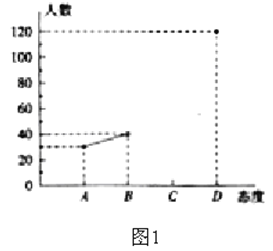
(1)此次抽样检查中,共调查了 名学生家长;
(2)将图1补充完整;
(3)根据抽样检查的结果,请你估计该市城区6000名中学生家长中有多少名家长持反对态度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司欲招聘一名公关人员,对甲、乙、丙、丁四位候选人进行了面试和笔试,他们的成绩如表:
候选人
甲
乙
丙
丁
测试成绩
(百分制)
面试
86
92
90
83
笔试
90
83
83
92
如果公司认为,作为公关人员面试的成绩应该比笔试的成绩更重要,并分别赋予它们
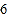 和
和 的权.根据四人各自的平均成绩,公司将录取( )
的权.根据四人各自的平均成绩,公司将录取( )A. 甲 B. 乙 C. 丙 D. 丁
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
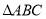 ,若
,若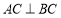 ,
,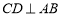 ,
,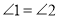 ,下列结论:①
,下列结论:①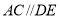 ;②
;②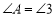 ;③
;③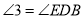 ;④
;④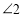 与
与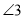 互补;⑤
互补;⑤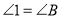 ,其中正确的有( )
,其中正确的有( )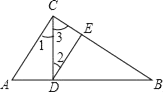
A.2个B.3个C.4个D.5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】常州每年举行一次“一袋牛奶的暴走”公益活动,用步行的方式募集善款,其中挑战型路线”的起点是淹城站,并沿着规定的线路到达终点吾悦国际站.甲、乙两组市民从起点同时出发,已知甲组的速度为6km/h,乙组的速度为5km/h,当甲组到达终点后,立即以3km/h的速度按原线路返回,并在途中的P站与乙组相遇,P站与吾悦国际站之间的路程为1.5km
(1)求“挑战型路线”的总长;
(2)当甲组到达终点时,乙组离终点还有多少路程?
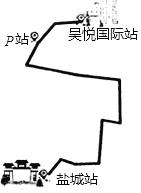
相关试题

