【题目】如图,在四边形ABCD中,∠D=90°,AB=2,BC=4,CD=AD= ![]() .
. 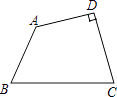
(1)求∠BAD、∠BCD的度数.
(2)求四边形ABCD的面积.
参考答案:
【答案】
(1)解:连接AC,如图所示:
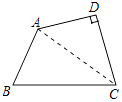
∵CD=AD= ![]() ,∠D=90°,
,∠D=90°,
∴∠DAC=∠ACD=45°,AC2=AD2+CD2=2×6=12.AC=2 ![]() ,
,
在△ABC中,∵AB2+BC2=22+12=16=AC2,
∴∠BAC=90°.
∵BC=2AB,
∴∠ACB=30°,
∴∠BAD=∠BAC+∠CAD=90°+45°=135°,∠BCD=∠ACB+∠ACD=30°+45°=75°
(2)解:四边形ABCD的面积=△ABC的面积+△ACD的面积 ![]() ×2×2
×2×2 ![]() +
+ ![]() ×
× ![]() ×
× ![]() =2
=2 ![]() +3.
+3.
【解析】(1)由等腰直角三角形的性质得出∠DAC=∠ACD=45°,AC2=AD2+CD2=2×6=12.AC=2 ![]() ,由勾股定理的逆定理证出∠BAC=90°.证出∠ACB=30°,即可得出所求;(2)四边形ABCD的面积=△ABC的面积+△ACD的面积,代入计算即可.
,由勾股定理的逆定理证出∠BAC=90°.证出∠ACB=30°,即可得出所求;(2)四边形ABCD的面积=△ABC的面积+△ACD的面积,代入计算即可.
【考点精析】认真审题,首先需要了解勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2),还要掌握勾股定理的逆定理(如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】江堤边一洼地发生了管涌,江水不断地涌出,假定每分钟涌出的水量相等,如果用两台抽水机抽水,40分钟可抽完;如果用4台抽水机抽水,16分钟可抽完,如果要在10分钟内抽完水,那么至少需要抽水机多少台.(1999年全国初中数学联合竞赛试题)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果x=3时,式子px3+qx+1的值为2016,则当x=﹣3时,式子px3+qx﹣1的值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)已知m=1+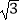 ,n=1﹣
,n=1﹣ 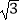 ,求代数式m2+2mn﹣n2的值;
,求代数式m2+2mn﹣n2的值;
(2)已知x+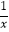 =
= 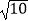 ,求代数式x﹣
,求代数式x﹣ 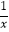 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某班开展安全知识竞赛,评分标准是答对一道题得5分,记作+5分,答错或不答一道题扣2分,记作﹣2分.竞赛共有20道题,小明答对了15道题,则小明得分_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法求二次函数y=-x2+2x+1的顶点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将自己的双手手掌印按在同一张纸上,两个手掌印____(填“能”或“不能”)通过平移完全重合在一起.
相关试题

