搜索
【题目】如图，沿矩形ABCD的对角线折叠，先折出折痕AC，再折叠AB，使AB落在对角线AC上，折痕AE，若AD=8，AB=6．则BE= ． 
参考答案：
【答案】3
【解析】解：如图所示：AB沿AE折叠后点B的对应点为F．
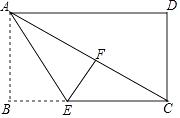
由勾股定理得，AC= 
= 
=10．
设BE=x，则CE=8﹣x．
由翻折的性质得：BE=EF=x，AF=AB=6，
所以CF=10﹣6=4．
在Rt△CEF中，由勾股定理得，EF2+CF2=CE2，即x2+42=（8﹣x）2，
解得x=3，即BE=3．
所以答案是：3．
【考点精析】解答此题的关键在于理解矩形的性质的相关知识，掌握矩形的四个角都是直角，矩形的对角线相等，以及对翻折变换（折叠问题）的理解，了解折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在扇形AOB中，∠AOB=90°，以点A为圆心，OA的长为半径作
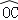交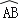 
于点C，若OA=2，则阴影部分的面积为 ．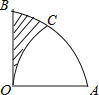 
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一次函数y=ax+b的图像与正比例函数y=kx的图像交于点M，
（1）求正比例函数和一次函数的解析式；
（2）根据图像写出使正比例函数的值大于一次函数的值的x的取值范围；
（3）求ΔMOP的面积。
-
科目： 来源： 题型：
查看答案和解析>>【题目】花园内有一块边长为a的正方形土地，园艺师设计了三种不同的图案，如图①②③所示，其中的阴影部分用于种植花草，试比较三种方案中用于种植花草部分的面积的大小，并用平移的知识说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某体育馆用大小相同的长方形木板镶嵌地面，第1次铺2块如图①；第2次把第1次铺的完全围起来，如图②，此时共使用木板12块；第3次把第2次铺的完全围起来，如图③：
（1）依此方法，第4次铺完后，共使用的木板数为______．
（2）依此方法，第10次铺完后，共使用的木板数为______．
（3）依此方法，第n次铺完后，共使用的木板数为______．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，平行四边形ABCD中，点E、F分别在AB、CD上，且BE=DF，EF与AC相交于点P，求证：PA=PC．
-
科目： 来源： 题型：
查看答案和解析>>【题目】按下面摆好的方式，并使用同一种图形，只通过平移方式就能进行平面镶嵌（即平面密铺）的有_______（写出所有正确答案的序号）．
相关试题
