【题目】如图,一居民楼底部B与山脚P位于同一水平线上,小李在P处测得居民楼顶A的仰角为60°,然后他从P处沿坡角为45°的山坡向上走到C处,这时点C与点A恰好在同一水平线上,点A、B、P、C在同一平面内.
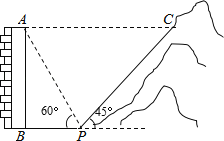
(1)若BP=10m,求居民楼AB的高度;(精确到0.1,![]() ≈1.732)
≈1.732)
(2)若PC=24m,求C、A之间的距离.
参考答案:
【答案】(1)17.3m;(2)(10![]() +12
+12![]() )m.
)m.
【解析】
试题分析:(1)在Rt△ABP中根据tan60°=![]() =
=![]() ,即可得到结论;
,即可得到结论;
(2)过点C作CE⊥BP于点E,在Rt△PCE中,根据cos45°=![]() =
=![]() =
=![]() ,得到PE=12
,得到PE=12![]() m,于是得到AC=BE=10
m,于是得到AC=BE=10![]() +12
+12![]() m.
m.
解:(1)在Rt△ABP中
∵PB=10m,∠APB=60°,
∴tan60°=![]() =
=![]() ,
,
∴AB=10![]() ≈17.3m,
≈17.3m,
答:居民楼AB的高度约为17.3;
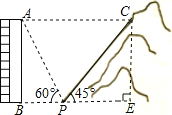
(2)过点C作CE⊥BP于点E,在Rt△PCE中,
∵∠CPE=45°,
∴cos45°=![]() =
=![]() =
=![]() ,
,
∴PE=12![]() m,
m,
∴AC=BE=10![]() +12
+12![]() m,
m,
答:C、A之间的距离约为(10![]() +12
+12![]() )m.
)m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B在⊙O上,点C在⊙O外,连接AB和OC交于D,且OB⊥OC,AC=CD.
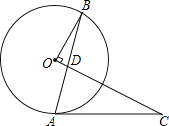
(1)判断AC与⊙O的位置关系,并证明你的结论;
(2)若OC=13,OD=1,求⊙O的半径及tanB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小马虎同学在计算某个多边形的内角和时得到1840°,老师说他算错了,于是小马虎认真地检查了一遍发现漏算了一个内角,求漏算的那个内角是多少度?这个多边形是几边形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的半径为5,⊙O的圆心为坐标原点,点A的坐标为(3,4),则点A与⊙O的位置关系是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个数m的平方根是3a+1和a+11,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC≌△DEF,且AB=4,BC=5,AC=6,则DE的长为( )
A. 4 B. 5 C. 6 D. 4或5或6
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC为等边三角形,D为BC延长线上的一点,CE平分∠ACD,CE=BD.
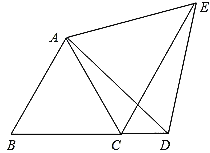
求证:(1)△ABD≌△ACE
(2)△ADE为等边三角形.
相关试题

