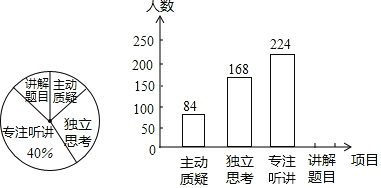
【题目】某市数学调研小组对老师在讲评试卷中学生参与的深度与广度进行评价调查,其评价项目为“主动质疑”、“独立思考”、“专注听讲”、“讲解题目”四项,该调研小组随机抽取了若干名初中七年级学生的参与情况,绘制成如图所示的频数分布直方图和扇形統计图(均不完整),请根据图中所给信息答下列问题:
(1)在这次评价中,一共抽查了 名学生;
(2)请将频数分布直方图补充完整;
(3)如果全市有4000名七年级学生,那么在试卷评讲课中,“独立思考”的七年级学生约有多少人?
参考答案:
【答案】(1)560;(2)频数分布直方图补充完整图见解析;(3)故在试卷讲评课中,“独立思考”的七年级生约有12000人.
【解析】
(1)由专注听讲的人数及其所占百分比可得总人数;
(2)根据各项目人数之和等于总人数可得讲解题目对应的人数,从而补全图形;
(3)利用样本估计总体思想求解可得.
(1)在这次评价中,一共抽查学生560人,
故答案为:560;
(2)“讲解题目”的人数是:![]() (人
(人![]() .
.
作图如下:
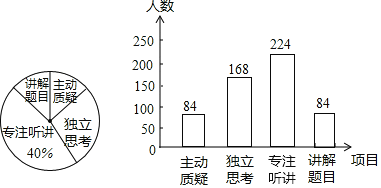
(3)![]() (人
(人![]()
故在试卷讲评课中,“独立思考”的七年级生约有12000人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列调查中,调查方式选择最合理的是


A. 为了解安徽省中学生的课外阅读情况,选择全面调查
B. 调查七年级某班学生打网络游戏的情况,选择抽样调查
C. 为确保长征六号遥二火箭成功发射,应对零部件进行全面调查
D. 为了解一批袋装食品是否含有防腐剂,选择全面调查
-
科目: 来源: 题型:
查看答案和解析>>【题目】“父母恩深重,恩怜无歇时”,每年5月的第二个星期日即为母亲节,节日前夕巴蜀中学学生会计划采购一批鲜花礼盒赠送给妈妈们.
(1)经过和花店卖家议价,可在原标价的基础上打八折购进,若在花店购买80个礼盒最多花费7680元,请求出每个礼盒在花店的最高标价;(用不等式解答)
(2)后来学生会了解到通过“大众点评”或“美团”同城配送会在(1)中花店最高售价的基础上降价25%,学生会计划在这两个网站上分别购买相同数量的礼盒,但实际购买过程中,“大众点评”网上的购买价格比原有价格上涨
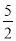 m%,购买数量和原计划一样:“美团”网上的购买价格比原有价格下降了
m%,购买数量和原计划一样:“美团”网上的购买价格比原有价格下降了 m元,购买数量在原计划基础上增加15m%,最终,在两个网站的实际消费总额比原计划的预算总额增加了
m元,购买数量在原计划基础上增加15m%,最终,在两个网站的实际消费总额比原计划的预算总额增加了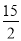 m%,求出m的值.
m%,求出m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,三角形ABC的顶点均在格点上,在建立平面直角坐标系后,点A的坐标为(2,4),点B的坐标为(1,1),点C的坐标为(3,2).
(1)将三角形ABC先沿着x轴负方向平移6个单位,再沿y轴负方向平移2个单位得到三角形A1B1C1,在图中画出三角形A1B1C1;
(2)分别写出A1,B1、C1的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).
(1)画出△ABC关于x轴的对称图形△A1B1C1;
(2)画出△A1B1C1沿x轴向右平移4个单位长度后得到的△A2B2C2;
(3)如果AC上有一点M(a,b)经过上述两次变换,那么对应A2C2上的点M2的坐标是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠BAC=90°,AH⊥BC于点H,过点C作CD⊥AC,连接AD,点M为AC上一点,且AM=CD,连接BM交AH于点N,交AD于点E.

(1)若AB=3,AD=
 ,求△BMC的面积;
,求△BMC的面积;(2)点E为AD的中点时,求证:AD=
 BN .
BN . -
科目: 来源: 题型:
查看答案和解析>>【题目】对于一个三位正整数t,将各数位上的数字重新排序后(包括本身),得到一个新的三位数
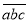 (a≤c),在所有重新排列的三位数中,当|a+c﹣2b|最小时,称此时的
(a≤c),在所有重新排列的三位数中,当|a+c﹣2b|最小时,称此时的  为t的“最优组合”,并规定F(t)=|a﹣b|﹣|b﹣c|,例如:124重新排序后为:142、214、因为|1+4﹣4|=1,|1+2﹣8|=5,|2+4﹣2|=4,所以124为124的“最优组合”,此时F(124)=﹣1.
为t的“最优组合”,并规定F(t)=|a﹣b|﹣|b﹣c|,例如:124重新排序后为:142、214、因为|1+4﹣4|=1,|1+2﹣8|=5,|2+4﹣2|=4,所以124为124的“最优组合”,此时F(124)=﹣1.(1)三位正整数t中,有一个数位上的数字是另外两数位上的数字的平均数,求证:F(t)=0;
(2)一个正整数,由N个数字组成,若从左向右它的第一位数能被1整除,它的前两位数能被2整除,前三位数能被3整除,…,一直到前N位数能被N整除,我们称这样的数为“善雅数”.例如:123的第一位数1能披1整除,它的前两位数12能被2整除,前三位数123能被3整除,则123是一个“善雅数”.若三位“善雅数”m=200+10x+y(0≤x≤9,0≤y≤9,x、y为整数),m的各位数字之和为一个完全平方数,求出所有符合条件的“善雅数”中F(m)的最大值.
相关试题

