【题目】如图正比例函数y=2x的图象与一次函数y=kx+b的图象交于点A(m,2),一次函数的图象经过点B(﹣2,﹣1)与y轴交点为C与x轴交点为D. 
(1)求一次函数的解析式;
(2)点P是x轴上一点,且△ADP的面积是△AOD面积的2倍,直接写出点P的坐标.
参考答案:
【答案】
(1)解:∵点A(m,2)在正比例函数y=2x的图象上,
∴2m=2,
∴m=1.
∴点A坐标为(1,2).
又∵点A、B在一次函数y=kx+b的图象上
∴ ![]() ,解得:
,解得: ![]() ,
,
∴一次函数解析式为y=x+1
(2)解:令y=x+1中y=0,则x=﹣1,
∴D(﹣1,0),
∴OD=1.
设点P的坐标为(n,0),
∵△ADP的面积是△AOD面积的2倍,
∴DP=|n﹣(﹣1)|=2OD=2,
解得:n=1或n=﹣3,
∴点P坐标为(1,0)或(﹣3,0)
【解析】(1)由点A在正比例函数图象上可得出关于m的一元一次方程,解方程即可得出点A的坐标,再根据点A、B的坐标利用待定系数法求出函数解析式;(2)根据直线AB的解析式求出点D的坐标,再根据三角形的面积公式结合△ADP的面积是△AOD面积的2倍,即可得出关于n的含绝对值符号的一元一次方程,解方程即可得出n的值,由此即可得出点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)求出y与x的函数关系式;
(2)当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?
(3)设该文具店每周销售这种纪念册所获得的利润为w元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于中心对称的两个图形,对称点的连线经过__________
-
科目: 来源: 题型:
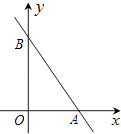
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知一次函数y=﹣2x+6的图象与x轴交于点A,与y轴交于点B.试求出△OAB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列乘法运算中不能用平方差公式计算的是( )
A. (x+1)(x-1) B. (x-1)(-x+1)
C. (-x+1)(-x-1) D. (x+1)(-x+1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】长方形的面积是3a2-3ab+6a,一边长为3a,则它的另一条边长为( )
A. 2a-b+2 B. a-b+2
C. 3a-b+2 D. 4a-b+2
-
科目: 来源: 题型:
查看答案和解析>>【题目】在甲、乙两个不透明的布袋,甲袋中装有3个完全相同的小球,分别标有数字0,1,2;乙袋中装有3个完全相同的小球,分别标有数字﹣1,﹣2,0;现从甲袋中随机抽取一个小球,记录标有的数字为x,再从乙袋中随机抽取一个小球,记录标有的数字为y,确定点M坐标为(x,y).
(1)用树状图或列表法列举点M所有可能的坐标;
(2)求点M(x,y)在函数y=-x+1的图象上的概率;
(3)在平面直角坐标系xOy中,⊙O的半径是2,求过点M(x,y)能作⊙O的切线的概率.
相关试题

