【题目】如图,在平面直角坐标系中,已知一次函数y=﹣2x+6的图象与x轴交于点A,与y轴交于点B.试求出△OAB的面积.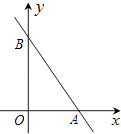
参考答案:
【答案】解:当y=0时,﹣2x+6=0,解得x=3,则A点坐标为(3,0);
∴OA=3;
当y=0时,y=﹣2x+6=6,则B点坐标为(0,6);
∴OB=6;
∴△OAB的面积= ![]()
【解析】根据坐标轴上点的坐标特征求A点和B点坐标,利用三角形面积公式解答即可.
【考点精析】解答此题的关键在于理解一次函数的图象和性质的相关知识,掌握一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数y=﹣
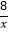 , 则有
, 则有
①它的图象在一、三象限:
②点(﹣2,4)在它的图象上;
③当l<x<2时,y的取值范围是﹣8<y<﹣4;
④若该函数的图象上有两个点A (x1 , y1),B(x2 , y2),那么当x1<x2时,y1<y2
以上叙述正确的是 -
科目: 来源: 题型:
查看答案和解析>>【题目】某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)求出y与x的函数关系式;
(2)当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?
(3)设该文具店每周销售这种纪念册所获得的利润为w元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于中心对称的两个图形,对称点的连线经过__________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图正比例函数y=2x的图象与一次函数y=kx+b的图象交于点A(m,2),一次函数的图象经过点B(﹣2,﹣1)与y轴交点为C与x轴交点为D.

(1)求一次函数的解析式;
(2)点P是x轴上一点,且△ADP的面积是△AOD面积的2倍,直接写出点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列乘法运算中不能用平方差公式计算的是( )
A. (x+1)(x-1) B. (x-1)(-x+1)
C. (-x+1)(-x-1) D. (x+1)(-x+1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】长方形的面积是3a2-3ab+6a,一边长为3a,则它的另一条边长为( )
A. 2a-b+2 B. a-b+2
C. 3a-b+2 D. 4a-b+2
相关试题

