Question

【题目】在甲、乙两个不透明的布袋，甲袋中装有3个完全相同的小球，分别标有数字0，1，2；乙袋中装有3个完全相同的小球，分别标有数字﹣1，﹣2，0；现从甲袋中随机抽取一个小球，记录标有的数字为x，再从乙袋中随机抽取一个小球，记录标有的数字为y，确定点M坐标为（x，y）．

（1）用树状图或列表法列举点M所有可能的坐标；

（2）求点M（x，y）在函数y=-x+1的图象上的概率；

（3）在平面直角坐标系xOy中，⊙O的半径是2，求过点M（x，y）能作⊙O的切线的概率．

Answer 1

【答案】（1）答案见试题解析；（2）；（3）．

【解析】试题分析：（1）用树状图法展示所有9种等可能的结果数；

（2）根据一次函数图象上点的坐标特征，从9个点中找出满足条件的点，然后根据概率公式计算；

（3）利用点与圆的位置关系找出圆上的点和圆外的点，由于过这些点可作⊙O的切线，则可计算出过点M（x，y）能作⊙O的切线的概率．

解：（1）画树状图：

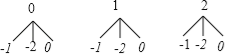
共有9种等可能的结果数，它们是：（0，﹣1），（0，﹣2），（0，0），（1，﹣1），（1，﹣2），（1，0），（2，﹣1），（2，﹣2），（2，0）；

（2）在直线y=﹣x+1的图象上的点有：（1，0），（2，﹣1），

所以点M（x，y）在函数y=﹣x+1的图象上的概率=；

（3）在⊙O上的点有（0，﹣2），（2，0），在⊙O外的点有（1，﹣2），（2，﹣1），（2，﹣2），

所以过点M（x，y）能作⊙O的切线的点有5个，

所以过点M（x，y）能作⊙O的切线的概率=．