【题目】已知抛物线y=ax2+bx﹣3经过(﹣1,0),(3,0)两点,与y轴交于点C,直线y=kx与抛物线交于A,B两点.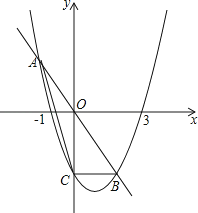
(1)写出点C的坐标并求出此抛物线的解析式;
(2)当原点O为线段AB的中点时,求k的值及A,B两点的坐标;
(3)是否存在实数k使得△ABC的面积为 ![]() ?若存在,求出k的值;若不存在,请说明理由.
?若存在,求出k的值;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:令抛物线y=ax2+bx﹣3中x=0,则y=﹣3,
∴点C的坐标为(0,﹣3).
∵抛物线y=ax2+bx﹣3经过(﹣1,0),(3,0)两点,
∴有 ![]() ,解得:
,解得: ![]() ,
,
∴此抛物线的解析式为y=x2﹣2x﹣3
(2)
解:将y=kx代入y=x2﹣2x﹣3中得:kx=x2﹣2x﹣3,
整理得:x2﹣(2+k)x﹣3=0,
∴xA+xB=2+k,xAxB=﹣3.
∵原点O为线段AB的中点,
∴xA+xB=2+k=0,
解得:k=﹣2.
当k=﹣2时,x2﹣(2+k)x﹣3=x2﹣3=0,
解得:xA=﹣ ![]() ,xB=
,xB= ![]() .
.
∴yA=﹣2xA=2 ![]() ,yB=﹣2xB=2
,yB=﹣2xB=2 ![]() .
.
故当原点O为线段AB的中点时,k的值为﹣2,点A的坐标为(﹣ ![]() ,2
,2 ![]() ),点B的坐标为(
),点B的坐标为( ![]() ,﹣2
,﹣2 ![]() )
)
(3)
解:假设存在.
由(2)可知:xA+xB=2+k,xAxB=﹣3,
S△ABC= ![]() OC|xA﹣xB|=
OC|xA﹣xB|= ![]() ×3×
×3× ![]() =
= ![]() ,
,
∴(2+k)2﹣4×(﹣3)=10,即(2+k)2+2=0.
∵(2+k)2非负,无解.
故假设不成了.
所以不存在实数k使得△ABC的面积为 ![]()
【解析】(1)令抛物线解析式中x=0求出y值即可得出C点的坐标,有点(﹣1,0)、(3,0)利用待定系数法即可求出抛物线的解析式;(2)将正比例函数解析式代入抛物线解析式中,找出关于x的一元二次方程,根据根与系数的关系即可得出“xA+xB=2+k,xAxB=﹣3”,结合点O为线段AB的中点即可得出xA+xB=2+k=0,由此得出k的值,将k的值代入一元二次方程中求出xA、xB , 在代入一次函数解析式中即可得出点A、B的坐标;(3)假设存在,利用三角形的面积公式以及(2)中得到的“xA+xB=2+k,xAxB=﹣3”,即可得出关于k的一元二次方程,结合方程无解即可得出假设不成了,从而得出不存在满足题意的k值.本题考查了待定系数法求函数解析式、根与系数的关系、解一元二次方程以及三角形的面积公式,解题的关键是:(1)利用待定系数法求出函数解析式;(2)结合根与系数的关系求出k值;(3)利用反正法找出方程无解.本题属于中档题,难度不大,解决该题型题目时,将正比例函数解析式代入二次函数解析式中,利用三角形的面积公式结合根与系数的关系找出关于k的方程是关键.
【考点精析】认真审题,首先需要了解抛物线与坐标轴的交点(一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.).
-
科目: 来源: 题型:
查看答案和解析>>【题目】数轴上点 A,B 到表示2 的点的距离都为 9,P 为线段 AB 上任一点,C,D 两点分别从 P,B 同时向 A 点移动,且 C 点运动速度为每秒 3 个单位长度,D 点运动速度为每秒 4 个单位长度,运动 3 秒时,CD=4,则 P 点表示的数为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读后解决问题:
在“15.3分式方程”一课的学习中,老师提出这样的一个问题:如果关于x的分式方程
 的解为正数,那么a的取值范围是什么?
的解为正数,那么a的取值范围是什么?经过交流后,形成下面两种不同的答案:
小明说:解这个关于x的分式方程,得到方程的解为x=a﹣2.
因为解是正数,可得a﹣2>0,所以a>2.
小强说:本题还要必须a≠3,所以a取值范围是a>2且a≠3.
(1)小明与小强谁说的对,为什么?
(2)关于x的方程
 有整数解,求整数m的值.
有整数解,求整数m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】近年来,随着我国的科学技术的迅猛发展,很多行业已经由“中国制造”升级为“中国创造”,高铁事业是“中国创造”的典范,一般的高铁包括G字头的高速动车组以及D字头的动车组.由大连到北京的G377的平均速度是D31的平均速度的1.2倍,行驶相同的路程1500千米,G377少用1个小时.
(1)求D31的平均速度.
(2)若以“速度与票价的比值”定义这两种列车的性价比,人们出行都喜欢选择性价比高的方式.现阶段D31票价为266元/张,G377票价为400元/张,如果你有机会给有关部门提一个合理化建议,使G377的性价比达到D31的性价比,你如何建议,为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在直角坐标系xOy中,点A在y轴上,点B,点C在x轴上,点C在点B的右侧,OA=2OB=2BC=2.
(1)点C的坐标是 ;
(2)点P是x轴上一点,点P到AC的距离等于AC的长度,求点P的坐标;
(3)如图2,点D是AC上一点,∠CBD=∠ABO,连接OD,在AB上是否存在一点Q,使QB=AB﹣OD,若存在,求点Q与点D的横坐标之和,若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】问题探究:
①新知学习
若把将一个平面图形分为面积相等的两个部分的直线叫做该平面图形的“面线”,其“面线”被该平面图形截得的线段叫做该平面图形的“面径”(例如圆的直径就是圆的“面径”).
②解决问题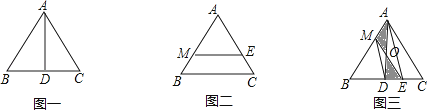
已知等边三角形ABC的边长为2.
(1)如图一,若AD⊥BC,垂足为D,试说明AD是△ABC的一条面径,并求AD的长;
(2)如图二,若ME∥BC,且ME是△ABC的一条面径,求面径ME的长;
(3)如图三,已知D为BC的中点,连接AD,M为AB上的一点(0<AM<1),E是DC上的一点,连接ME,ME与AD交于点O,且S△MOA=S△DOE .
①求证:ME是△ABC的面径;
②连接AE,求证:MD∥AE;
(4)请你猜测等边三角形ABC的面径长l的取值范围(直接写出结果) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在Rt△ABC中,∠ABC=90°,点D沿BC自B向C运动(点D与点B、C不重合),作BE⊥AD于E,CF⊥AD于F,则BE+CF的值( )
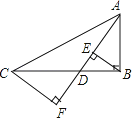
A.不变
B.增大
C.减小
D.先变大再变小
相关试题

