【题目】问题探究:
①新知学习
若把将一个平面图形分为面积相等的两个部分的直线叫做该平面图形的“面线”,其“面线”被该平面图形截得的线段叫做该平面图形的“面径”(例如圆的直径就是圆的“面径”).
②解决问题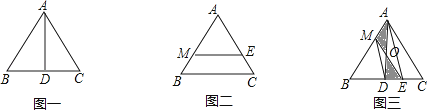
已知等边三角形ABC的边长为2.
(1)如图一,若AD⊥BC,垂足为D,试说明AD是△ABC的一条面径,并求AD的长;
(2)如图二,若ME∥BC,且ME是△ABC的一条面径,求面径ME的长;
(3)如图三,已知D为BC的中点,连接AD,M为AB上的一点(0<AM<1),E是DC上的一点,连接ME,ME与AD交于点O,且S△MOA=S△DOE .
①求证:ME是△ABC的面径;
②连接AE,求证:MD∥AE;
(4)请你猜测等边三角形ABC的面径长l的取值范围(直接写出结果)
参考答案:
【答案】
(1)
解:如图一中,
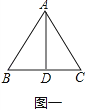
∵AB=AC=BC=2,AD⊥BC,
∴BD=DC,
∴S△ABD=S△ADC,
∴线段AD是△ABC的面径.
∵∠B=60°,
∴sin60°= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴AD= ![]() .
.
(2)
解:如图二中,
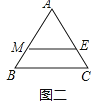
∵ME∥BC,且ME是△ABC的一条面径,
∴△AME∽△ABC, ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴ME= ![]() .
.
(3)
解:如图三中,作MN⊥AE于N,DF⊥AE于F.
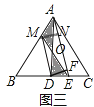
∵S△MOA=S△DOE,
∴S△AEM=S△AED,
∴ ![]() AEMN=
AEMN= ![]() AEDF,
AEDF,
∴MN=DF,
∵MN∥DF,
∴四边形MNFD是平行四边形,
∴DM∥AE.
(4)
解:如图四中,作MF⊥BC于F,设BM=x,BE=y,
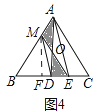
∵DM∥AE,
∴ ![]() ,
,
∴ ![]() ,
,
∴xy=2,
在RT△MBF中,∵∠MFB=90°,∠B=60°,BM=x,
∴BF= ![]() x,MF=
x,MF= ![]() x,
x,
∴ME= ![]() =
= ![]() =
= ![]() ≥
≥ ![]() ,
,
∴ME≥ ![]() ,
,
∵ME是等边三角形面径,AD也是等边三角形面积径,
∴等边三角形ABC的面径长l的取值范围 ![]() ≤l≤
≤l≤ ![]()
【解析】(1)根据等腰三角形三线合一即可证明,利用直角三角形30°性质,即可求出AD.(2)根据相似三角形性质面积比等于相似比的平方,即可解决问题.(3)如图三中,作MN⊥AE于N,DF⊥AE于F,先证明MN=DF,推出四边形MNFD是平行四边形即可.(4)如图四中,作MF⊥BC于F,设BM=x,BE=y,求出EM,利用不等式性质证明ME≥ ![]() 即可解决问题.本题考查等边三角形的性质、平行线的性质,三角形面积等知识,解题的关键是理解题意,学会条件常用辅助线,记住不等式的性质x2+y2≥2xy,属于中考压轴题.
即可解决问题.本题考查等边三角形的性质、平行线的性质,三角形面积等知识,解题的关键是理解题意,学会条件常用辅助线,记住不等式的性质x2+y2≥2xy,属于中考压轴题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】近年来,随着我国的科学技术的迅猛发展,很多行业已经由“中国制造”升级为“中国创造”,高铁事业是“中国创造”的典范,一般的高铁包括G字头的高速动车组以及D字头的动车组.由大连到北京的G377的平均速度是D31的平均速度的1.2倍,行驶相同的路程1500千米,G377少用1个小时.
(1)求D31的平均速度.
(2)若以“速度与票价的比值”定义这两种列车的性价比,人们出行都喜欢选择性价比高的方式.现阶段D31票价为266元/张,G377票价为400元/张,如果你有机会给有关部门提一个合理化建议,使G377的性价比达到D31的性价比,你如何建议,为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx﹣3经过(﹣1,0),(3,0)两点,与y轴交于点C,直线y=kx与抛物线交于A,B两点.
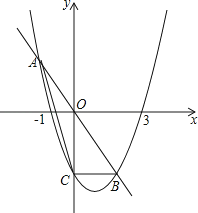
(1)写出点C的坐标并求出此抛物线的解析式;
(2)当原点O为线段AB的中点时,求k的值及A,B两点的坐标;
(3)是否存在实数k使得△ABC的面积为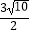 ?若存在,求出k的值;若不存在,请说明理由.
?若存在,求出k的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在直角坐标系xOy中,点A在y轴上,点B,点C在x轴上,点C在点B的右侧,OA=2OB=2BC=2.
(1)点C的坐标是 ;
(2)点P是x轴上一点,点P到AC的距离等于AC的长度,求点P的坐标;
(3)如图2,点D是AC上一点,∠CBD=∠ABO,连接OD,在AB上是否存在一点Q,使QB=AB﹣OD,若存在,求点Q与点D的横坐标之和,若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在Rt△ABC中,∠ABC=90°,点D沿BC自B向C运动(点D与点B、C不重合),作BE⊥AD于E,CF⊥AD于F,则BE+CF的值( )
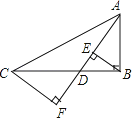
A.不变
B.增大
C.减小
D.先变大再变小 -
科目: 来源: 题型:
查看答案和解析>>【题目】将长为 1,宽为 a 的长方形纸片(0.5<a<1)如图折叠,剪下一个边长等于长方形的宽度的正方形(称为第一次操作);再把剩下的长方形如图折叠,剪下一个边长等于此时长方形宽度的正方形 (称为第二次操作);如此反复操作下去,如此反复下去,若在第 n 次操作后剩下的长方形恰好为正方形,则操作终止.

(1)第一次操作后,剩下的长方形两边长分别为 ;(用含 a 的代数式表示)
(2)若第二次操作后,剩下的长方形恰好是正方形,则求 a 的值,写出解答过程;
(3)若第三次操作后,剩下的长方形恰好是正方形,画出示意图形,直接写出 a 的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个底面直径为 5cm,高为 18cm 的圆柱形瓶内装满水,再将瓶内得水倒入一个底面直径为 6cm,高为 10cm 的圆柱形玻璃杯中,能否完全装下? 若装不下,那么瓶内水面还有多高? 若未能装满,求杯内水面离杯口的距离.
相关试题

