【题目】如图,将边长为4的正方形![]() 纸片沿
纸片沿![]() 折叠,点
折叠,点![]() 落在
落在![]() 边上的点
边上的点![]() 处,点
处,点![]() 与点
与点![]() 重合,
重合, ![]() 与
与![]() 交于点
交于点![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,则
,则![]() 的周长最小值是__________.
的周长最小值是__________.

参考答案:
【答案】![]()
【解析】
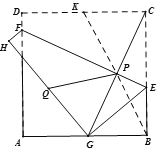
如图,取CD中点K,连接PK,PB,则CK=2,由折叠的性质可得PG=PC,GH=DC=4,PQ=PK,BP=PG,QG=2,要求△PGQ周长的最小值,只需求PQ+PG的最小值即可,即求PK+PB的最小值,观察图形可知,当K、P、B共线时,PK+PB的值最小,据此根据勾股定理进行求解即可得答案.
如图,取CD中点K,连接PK,PB,
则CK=![]() =2,
=2,
∵四边形ABCD是正方形,∴∠ABC=90°,
∵将边长为4的正方形ABCD纸片沿EF折叠,点C落在AB边上的点G处,点D与点H重合, CG与EF交于点P,取GH的中点Q,
∴PG=PC,GH=DC=4,PQ=PK,
∴BP=PG,QG=2,
要求△PGQ周长的最小值,只需求PQ+PG的最小值即可,
即求PK+PB的最小值,
观察图形可知,当K、P、B共线时,PK+PB的值最小,
此时,PK+PB=BK=![]() ,
,
∴△PGQ周长的最小值为:PQ+PG+QG= PK+PB+QG=BK+QG=2![]() +2,
+2,
故答案为:2![]() +2.
+2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
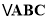 中,
中,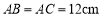 ,
,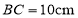 ,点D为AB的中点.如果点P在线段BC上以2cm/s的速度由点B向C点运动,同时,点Q在线段AC上由点A向C点以4cm/s的速度运动.
,点D为AB的中点.如果点P在线段BC上以2cm/s的速度由点B向C点运动,同时,点Q在线段AC上由点A向C点以4cm/s的速度运动.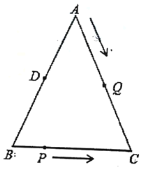
(1)若点P、Q两点分别从B、A两点同时出发,经过2秒后,
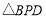 与
与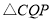 是否全等?请说明理由;
是否全等?请说明理由;(2)若点P、Q两点分别从B、A两点同时出发,
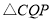 的周长为16cm,设运动时间为t,问:当t为何值时,是等腰三角形?
的周长为16cm,设运动时间为t,问:当t为何值时,是等腰三角形? -
科目: 来源: 题型:
查看答案和解析>>【题目】某乡村距城市50km,甲骑自行车从乡村出发进城,出发1小时30分后,乙骑摩托车也从乡村出发进城,结果比甲先到1小时,已知乙的速度是甲的2.5倍,求甲、乙两人的速度。
【答案】甲速12km/h,乙速30km/h.
【解析】试题分析:设甲的速度是
 则乙的速度是
则乙的速度是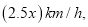 甲、乙所用时间分别为:
甲、乙所用时间分别为:  小时、
小时、 小时;根据题意可得甲比乙多用2.5小时,从而可得关于
小时;根据题意可得甲比乙多用2.5小时,从而可得关于 的方程,解方程即可解答此题;注意,最后要结合题意验根.
的方程,解方程即可解答此题;注意,最后要结合题意验根.试题解析:设甲的速度是
 则乙的速度是
则乙的速度是 根据题意列方程,得
根据题意列方程,得 整理,得
整理,得 ,
,解得:

经检验,
 是原方程的解.
是原方程的解.则

答:甲的速度是12km/h,乙的速度是30km/h.
【题型】解答题
【结束】
24【题目】已知
 求
求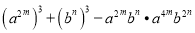 的值 。
的值 。 -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙三个教师承担本学期期末考试的第17题的网上阅卷任务,若由这三人中的某一人独立完成阅卷任务,则甲需要15小时,乙需要10小时,丙需要8小时。
(1)如果甲、乙、丙三人同时改卷,那么需要多少时间完成?
(2)如果按照甲、乙、丙、甲、乙、丙、……的次序轮流阅卷,每一轮中每人各阅卷1小时。那么要多少小时完成?
(3)能否把(2)题所说的甲、乙、丙的次序作适当调整,其余的不变,使得完成这项任务的时间至少提前半小时?(答题要求:如认为不能,需要说明理由;如认为能,请至少说出一种轮流的次序,并求出相应能提前多少时间完成阅卷任务)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1,(1)abc>0;(2)4a+2b+c>0;(3)4ac﹣b2<16a;(4)
 <a<
<a< ;(5)b<c,其中正确的结论有( )
;(5)b<c,其中正确的结论有( )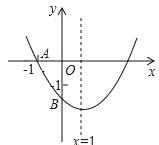
A. (2)(3)(4)(5) B. (1)(3)(4)(5) C. (1)(3)(4) D. (1)(2)(5)
-
科目: 来源: 题型:
查看答案和解析>>【题目】将4个数a,b,c,d排成2行、2列,两边各加一条竖直线记成
 ,定义
,定义 =ad-bc,上述记号就叫做2阶行列式.若
=ad-bc,上述记号就叫做2阶行列式.若 =-20,求x的值.
=-20,求x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了提高学生书写汉字的能力,增强保护汉字的意识,某校举办了“汉字听写大赛”,学生经选拔后进入决赛,测试同时听写100个汉字,每正确听写出一个汉字得1分,本次决赛,学生成绩为
 (分),且
(分),且 (无满分),将其按分数段分为五组,绘制出以下不完整表格:
(无满分),将其按分数段分为五组,绘制出以下不完整表格:组别
成绩
 (分)
(分)频数(人数)
频率
一

2

二

10
0.2
三

12

四


0.4
五

6


请根据表格提供的信息,解答以下问题:
(1)本次决赛共有__________名学生参加;
(2)直接写出表中:
 ___________
___________ ____________
____________(3)请补全右面相应的频数分布直方图;
(4)若决赛成绩不低于80分为优秀,则本次大赛的优秀率为__________.
相关试题

