【题目】如图,在等腰直角△ABC中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P,则下列结论:①图中全等的三角形只有两对;②△ABC的面积等于四边形CDOE面积的2倍;③OD=OE;④CE+CD=BC,其中正确的结论有( )

A.1个 B.2个 C.3个 D.4个
参考答案:
【答案】C
【解析】
试题分析:结论①错误.因为图中全等的三角形有3对;
结论②正确.由全等三角形的性质可以判断;
结论③正确.利用全等三角形的性质可以判断.
结论④正确.利用全等三角形和等腰直角三角形的性质可以判断.
解:结论①错误.理由如下:
图中全等的三角形有3对,分别为△AOC≌△BOC,△AOD≌△COE,△COD≌△BOE.
由等腰直角三角形的性质,可知OA=OC=OB,易得△AOC≌△BOC.
∵OC⊥AB,OD⊥OE,
∴∠AOD=∠COE.
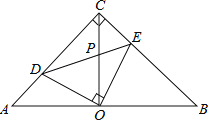
在△AOD与△COE中,
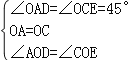 ,
,
∴△AOD≌△COE(ASA).
同理可证:△COD≌△BOE.
结论②正确.理由如下:
∵△AOD≌△COE,
∴S△AOD=S△COE,
∴S四边形CDOE=S△COD+S△COE=S△COD+S△AOD=S△AOC=![]() S△ABC,
S△ABC,
即△ABC的面积等于四边形CDOE的面积的2倍.
结论③正确,理由如下:∵△AOD≌△COE,
∴OD=OE;
结论④正确,理由如下:
∵△AOD≌△COE,
∴CE=AD,
∵AB=AC,
∴CD=EB,
∴CD+CE=EB+CE=BC.
综上所述,正确的结论有3个.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】252636"+1141542"= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个三角形的三条边长分别为1、2、x,则x的取值范围是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,点D是BC的中点,点E是AD上任意一点.
(1)如图1,连接BE、CE,问:BE=CE成立吗?并说明理由;
(2)如图2,若∠BAC=45°,BE的延长线与AC垂直相交于点F时,问:EF=CF成立吗?并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,ABCD是边长为60cm的正方形硬纸片,切去四个全等的等腰直角三角形(阴影部分所示),其中E,F在AB上;再沿虚线折起,点A,B,C,D恰好重合于点O处(如图②所示),形成有一个底面为正方形GHMN的包装盒,设AE=x (cm).
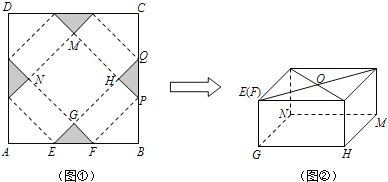
(1)求线段GF的长;(用含x的代数式表示)
(2)当x为何值时,矩形GHPF的面积S (cm2)最大?最大面积为多少?
(3)试问:此种包装盒能否放下一个底面半径为15cm,高为10cm的圆柱形工艺品,且使得圆柱形工艺品的一个底面恰好落在图②中的正方形GHMN内?若能,请求出满足条件的x的值或范围;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线y=﹣2x+8与x轴、y轴分别交于点A、C,以OA、OC为边在第一象限内作长方形OABC.
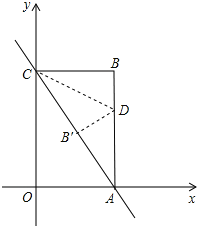
(1)求点A、C的坐标;
(2)将△ABC对折,使得点A的与点C重合,折痕交AB于点D,求直线CD的解析式;
(3)在(2)的条件下,坐标平面内是否存在点P(除点B外),使得△APC与△ABC全等?若存在,直接写出符合条件的点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.3a+4b=7ab B.(ab3)3=ab6 C.(a+2)2=a2+4 D.x12÷x6=x6
相关试题

