【题目】如果一条直线把一个平面图形的面积分成相等的两部分,我们把这条直线称为这个平面图形的一条面积等分线.
(1)平行四边形有_________条面积等分线;
(2)如图,四边形ABCD中,AB与CD不平行,AB≠CD, 且S△ABC<S△ACD,过点A画出四边形ABCD的面积等 分线,并写出理由._________.

参考答案:
【答案】(1)无数条;(2)理由见解析.
【解析】试题分析:(1)只要过两条对角线的交点的直线都可以把平行四边形的面积分成2个相等的部分;
(2)过点B作BE∥AC交DC的延长线于点E,连接AE.根据“△ABC和△AEC的公共边AC上的高也相等”推知S△ABC=S△AEC;然后由“割补法”可以求得S四边形ABCD=S△ACD+S△ABC=S△ACD+S△AEC=S△AED.
试题解析:(1)只要过两条对角线的交点的直线都可以把平行四边形的面积分成2个相等的部分,
则平行四边形有无数条面积等分线.
如图所示.

过点B作BE∥AC交DC的延长线于点E,连接AE.
∵BE∥AC,
∴△ABC和△AEC的公共边AC上的高也相等,
∴有S△ABC=S△AEC,
∴S四边形ABCD=S△ACD+S△ABC=S△ACD+S△AEC=S△AED;
∵S△ACD>S△ABC,
所以面积等分线必与CD相交,取DE中点F,则直线AF即为要求作的四边形ABCD的面积等分线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学对本校学生为抗震救灾自愿捐款活动进行了抽样调查,得到了一组学生捐款情况的数据.下图是根据这组数据绘制的统计图,根据图表回答下列各问:
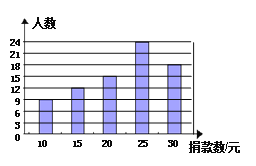
(1)求学校一共抽样调查的人数;
(2)求这组数据的众数、中位数;
(3)若该校共有1170名学生,估计全校学生共捐款多少元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】种植草莓大户张华有22吨草莓待售,现有两种销售渠道:一是运往省城成都直接批发给零售商;二是在遂宁本地市场零售. 经过调查分析,这两种销售渠道每天的销售量以及每吨所获纯利润见下表:
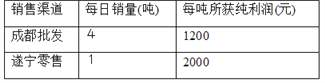
受客观因素和保质期影响,每天只能采用一种销售渠道并且必须在10日内将22吨草莓全部售出.
(1)设将
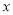 吨草莓运往成都批发给零售商,其余在遂宁零售,请写出销售完22吨草莓所获纯利润
吨草莓运往成都批发给零售商,其余在遂宁零售,请写出销售完22吨草莓所获纯利润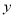 (元)与
(元)与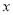 (吨)之间的函数关系式;
(吨)之间的函数关系式;(2)由于草莓必须在10日内售完,请你求出
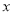 的取值范围;
的取值范围;(3)怎样安排这22吨草莓的销售渠道,才能使所获纯利润最大?并求出最大纯利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中,  是
是 边上的中线,
边上的中线, 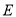 是
是 的中点,过点
的中点,过点 作
作 的平行线交
的平行线交 的延长线于点
的延长线于点 ,连结
,连结 和
和 .
.(1)求证:四边形
 是平行四边形;
是平行四边形;(2)若
 ,试判断四边形
,试判断四边形 的形状,并证明你的结论;
的形状,并证明你的结论;(3)
 是什么三角形时,四边形
是什么三角形时,四边形 是正方形,请说明理由.
是正方形,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若A=(2﹣1)(2+1)(22+1)(24+1)…(232+1)+1,则A的个位数字是__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数学活动课中,小强为了测量校园内旗杆AB的高度,站在教学楼上的C处测得旗杆底端B的俯角为45°,测得旗杆顶端A的仰角为30°,若旗杆与教学楼的水平距离CD为9米,则旗杆的高度是多少米?(
 ,结果保留整数)
,结果保留整数)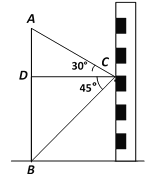
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在△ABC中,BF、CF是角平分线,DE∥BC,分别交AB、AC于点D、E,DE经过点F.结论:①△BDF和△CEF都是等腰三角形;②DE=BD+CE; ③△ADE的周长=AB+AC;④BF=CF.其中正确的是______.(填序号)

相关试题

