【题目】种植草莓大户张华有22吨草莓待售,现有两种销售渠道:一是运往省城成都直接批发给零售商;二是在遂宁本地市场零售. 经过调查分析,这两种销售渠道每天的销售量以及每吨所获纯利润见下表:
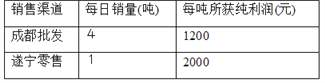
受客观因素和保质期影响,每天只能采用一种销售渠道并且必须在10日内将22吨草莓全部售出.
(1)设将![]() 吨草莓运往成都批发给零售商,其余在遂宁零售,请写出销售完22吨草莓所获纯利润
吨草莓运往成都批发给零售商,其余在遂宁零售,请写出销售完22吨草莓所获纯利润![]() (元)与
(元)与![]() (吨)之间的函数关系式;
(吨)之间的函数关系式;
(2)由于草莓必须在10日内售完,请你求出![]() 的取值范围;
的取值范围;
(3)怎样安排这22吨草莓的销售渠道,才能使所获纯利润最大?并求出最大纯利润.
参考答案:
【答案】(1)![]() (元)与
(元)与![]() (吨)之间的函数关系式是y=-800
(吨)之间的函数关系式是y=-800![]() +44000;
+44000;
(2)16≤![]() ≤22;
≤22;
(3)应安排16吨草莓运往成都批发给零售商,其余6吨草莓在遂宁零售,才能使所获纯利润最大,最大纯利润是31200元.
【解析】试题分析:(1)根据利润的关系,可得函数解析式;
(2)根据销售时间的关系,可得不等式组,根据解不等式组,可得答案;
(3)根据一次函数的性质,可得答案.
试题解析:(1)![]() (元)与
(元)与![]() (吨)之间的函数关系式是y=1200
(吨)之间的函数关系式是y=1200![]() +2000(22-
+2000(22-![]() ),即
),即![]() =-800
=-800![]() +44000;
+44000;
(2)根据题意,得: 
解得:16≤![]() ≤22;
≤22;
(3)∵一次函数![]() =-800
=-800![]() +44000中,
+44000中, ![]() =-800<0,
=-800<0,
∴![]() 随
随![]() 的增大而减小,
的增大而减小,
因此,当![]() =16时,
=16时, ![]() 的最大值=-800×16+44000=31200
的最大值=-800×16+44000=31200
∴应安排16吨草莓运往成都批发给零售商,其余6吨草莓在遂宁零售,才能使所获纯利润最大,最大纯利润是31200元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
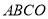 的顶点
的顶点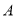 和
和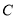 分别在
分别在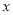 轴和
轴和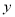 轴上,并且
轴上,并且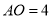 ,
, 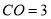 ,反比例函数
,反比例函数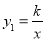 (
(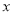 >0)的图象交
>0)的图象交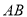 于点
于点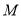 ,交
,交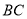 于点
于点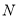 , 一次函数
, 一次函数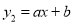 的图象经过点
的图象经过点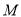 、
、 ,连结
,连结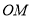 ,
, 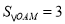 .
.(1)点
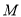 的坐标是( ),点
的坐标是( ),点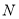 的坐标是( );
的坐标是( );(2)求反比例函数与一次函数的解析式;
(3)根据图象写出使得
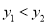 的
的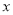 的取值范围.
的取值范围.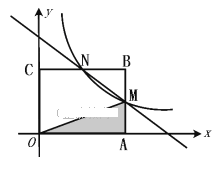
-
科目: 来源: 题型:
查看答案和解析>>【题目】小军用100元去买单价为4元的笔记本,他买完笔记本之后剩余的钱y(元)与买这种笔记本数量x(本)之间的关系式为 _________________
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学对本校学生为抗震救灾自愿捐款活动进行了抽样调查,得到了一组学生捐款情况的数据.下图是根据这组数据绘制的统计图,根据图表回答下列各问:
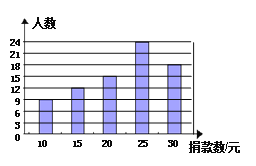
(1)求学校一共抽样调查的人数;
(2)求这组数据的众数、中位数;
(3)若该校共有1170名学生,估计全校学生共捐款多少元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中,  是
是 边上的中线,
边上的中线, 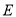 是
是 的中点,过点
的中点,过点 作
作 的平行线交
的平行线交 的延长线于点
的延长线于点 ,连结
,连结 和
和 .
.(1)求证:四边形
 是平行四边形;
是平行四边形;(2)若
 ,试判断四边形
,试判断四边形 的形状,并证明你的结论;
的形状,并证明你的结论;(3)
 是什么三角形时,四边形
是什么三角形时,四边形 是正方形,请说明理由.
是正方形,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一条直线把一个平面图形的面积分成相等的两部分,我们把这条直线称为这个平面图形的一条面积等分线.
(1)平行四边形有_________条面积等分线;
(2)如图,四边形ABCD中,AB与CD不平行,AB≠CD, 且S△ABC<S△ACD,过点A画出四边形ABCD的面积等 分线,并写出理由._________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若A=(2﹣1)(2+1)(22+1)(24+1)…(232+1)+1,则A的个位数字是__.
相关试题

