【题目】已知关于x,y的方程组 ![]() 的解为正数,则|k﹣6|+|k+1|= .
的解为正数,则|k﹣6|+|k+1|= .
参考答案:
【答案】7
【解析】解: ![]() ,
,
①+②得:2x=6k+4,即x=3k+2,
①﹣②得:2y=﹣2k+10,即y=﹣k+5,
根据题意得: ![]() ,
,
解得:﹣ ![]() <k<5,
<k<5,
∴k﹣6<0,k+1>0,
则原式=6﹣k+k+1=7,
所以答案是:7
【考点精析】掌握二元一次方程组的解和一元一次不等式组的解法是解答本题的根本,需要知道二元一次方程组中各个方程的公共解,叫做这个二元一次方程的解;解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分10分)如图,将□ABCD沿过点A的直线
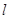 折叠,使点D落到AB边上的点
折叠,使点D落到AB边上的点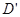 处,折痕
处,折痕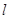 交CD边于点E,连接BE
交CD边于点E,连接BE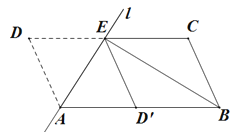
(1)求证:四边形
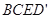 是平行四边形
是平行四边形(2)若BE平分∠ABC,求证:
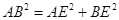
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.试探索BF与CF的数量关系,写出你的结论并证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,已知AB=AC,AB的垂直平分线交AB于点N,交AC于点M,连接MB.
(1)若∠ABC=70°,则∠NMA的度数是 度.
(2)若AB=8cm,△MBC的周长是14cm.
①求BC的长度;
②若点P为直线MN上一点,请你直接写出△PBC周长的最小值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,BC=16cm,AC=12cm,点P从点B出发,沿BC以2cm/s的速度向点C移动,点Q从点C出发,以1cm/s的速度向点A移动,若点P、Q分别从点B、C同时出发,设运动时间为t s,当t=时,△CPQ与△CBA相似.
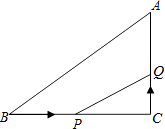
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A是线段DE上一点,∠BAC=90°,AB=AC,BD⊥DE,CE⊥DE.
(1)求证:DE=BD+CE.
(2)如果是如图2这个图形,BD、CE、DE有什么数量关系?并证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】现定义新运算“△”,对于任意有理数a,b,都有a△b=a2-ab+b,例如:3△5=32-3×5+5=-1,请根据上述知识解决问题:
(1)化简:(x-1)△(2+x);
(2)若(1)中的代数式的值大于6而小于9,求x的取值范围.
相关试题

