【题目】如图,已知在直角梯形AOBC中,AC∥OB,CB⊥OB,OB=18,BC=12,AC=9,对角线OC、AB交于点D,点E、F、G分别是CD、BD、BC的中点,以O为原点,直线OB为x轴建立平面直角坐标系,则G、E、D、F四个点中与点A在同一反比例函数图象上的是( )

A. 点G B. 点E C. 点D D. 点F
参考答案:
【答案】A
【解析】如下图,过点D作DM⊥OB于点M,则∠OME=90°,
∵在直角梯形AOBC中,AC∥OB,CB⊥OB,OB=18,BC=12,AC=9,
∴点A的坐标为(9,12),点B的坐标为(18,0),点C的坐标为(18,12),∠OBC=90°=∠ACB,△ACD∽△BDO,△OMD∽△OBC,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴DM=8,OM=12,
∴点D的坐标为(12,8),
∵点点E、F、G分别是CD、BD、BC的中点,
∴点E、F、G的坐标分别为(15,10)、(15,4)、(18,6),
∵在点A(9,12)中,9×12=108;点E(15,10)中,15×10=150;点F(15,4)中,15×4=60;点G(18,6)中18×6=1-8;
∴点A和点G中同一反比例函数的图象上.
故选A.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是小东设计的“作△ABC中BC边上的高线”的尺规作图过程.
已知:△ABC.
求作:△ABC中BC边上的高线AD.
作法:如图,
①以点B为圆心,BA的长为半径作弧,以点C为圆心,CA的长为半径作弧,两弧在BC下方交于点E;
②连接AE交BC于点D.
所以线段AD是△ABC中BC边上的高线.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵ =BA, =CA,
∴点B,C分别在线段AE的垂直平分线上( )(填推理的依据).
∴BC垂直平分线段AE.
∴线段AD是△ABC中BC边上的高线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题的提出:
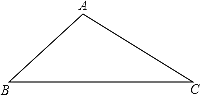
如果点P是锐角△ABC内一动点,如何确定一个位置,使点P到△ABC的三顶点的距离之和PA+PB+PC的值为最小?
问题的转化:
(1)把ΔAPC绕点A逆时针旋转60度得到
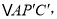 连接
连接 这样就把确定PA+PB+PC的最小值的问题转化成确定
这样就把确定PA+PB+PC的最小值的问题转化成确定 的最小值的问题了,请你利用如图证明:
的最小值的问题了,请你利用如图证明: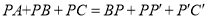 ;
;问题的解决:
(2)当点P到锐角△ABC的三项点的距离之和PA+PB+PC的值为最小时,请你用一定的数量关系刻画此时的点P的位置:_____________________________;
问题的延伸:
(3)如图是有一个锐角为30°的直角三角形,如果斜边为2,点P是这个三角形内一动点,请你利用以上方法,求点P到这个三角形各顶点的距离之和的最小值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:
在平面直角坐标系中,二元一次方程x-y=0的一个解
 可以用一个点(1,1)表示,二元一次方程有无数个解,以方程x-y=0的解为坐标的点的全体叫作方程x-y=0的图象。一般地,在平面直角坐标系中,任何一个二元一次方程的图象都是一条直线,我们可以把方程x-y=0的图象称为直线x-y=0。
可以用一个点(1,1)表示,二元一次方程有无数个解,以方程x-y=0的解为坐标的点的全体叫作方程x-y=0的图象。一般地,在平面直角坐标系中,任何一个二元一次方程的图象都是一条直线,我们可以把方程x-y=0的图象称为直线x-y=0。直线x-y=0把坐标平面分成直线上方区域,直线上,直线下方区域三部分,如果点M(x0,y0)的坐标满足不等式x-y≤0,那么点M(x0,y0)就在直线x-y=0的上方区域内。特别地,x=k(k为常数)表示横坐标为k的点的全体组成的一条直线,y=m(m为常数)表示纵坐标为m的点的全体组成的一条直线。
请根据以上材料,探索完成以下问题:
(1)已知点A(2,1)、B(
 ,
, )、C(
)、C( ,
, )、D(4,
)、D(4, ),其中在直线3x-2y=4上的点有 ;请再写出直线3x-2y=4上一个点的坐标 ;
),其中在直线3x-2y=4上的点有 ;请再写出直线3x-2y=4上一个点的坐标 ;(2)已知点P(x,y)的坐标满足不等式组
 ,则所有的点P组成的图形的面积是 ;
,则所有的点P组成的图形的面积是 ;(3)已知点P(x,y)的坐标满足不等式组
 ,请在平面直角坐标系中画出所有的点P组成的图形(涂上阴影),并直接写出上述图形的面积 。
,请在平面直角坐标系中画出所有的点P组成的图形(涂上阴影),并直接写出上述图形的面积 。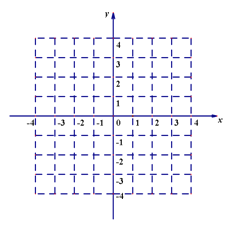
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在方格纸中(小正方形的边长为1),反比例函数y=
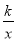 与直线的交点A、B均在格点上,根据所给的直角坐标系(O是坐标原点),解答下列问题:
与直线的交点A、B均在格点上,根据所给的直角坐标系(O是坐标原点),解答下列问题: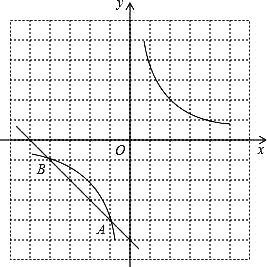
(1)分别写出点A、B的坐标后,把直线AB向右平移5个单位,再向上平移5个单位,画出平移后的直线A′B′;
(2)若点C在函数y=
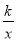 的图象上,△ABC是以AB为底的等腰三角形,请写出点C的坐标.
的图象上,△ABC是以AB为底的等腰三角形,请写出点C的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为2,点E、F分别为边AD、BC上的点,EF=
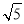 ,点G、H分别为AB、CD边上的点,连接GH,若线段GH与EF的夹角为45°,则GH的长为( )
,点G、H分别为AB、CD边上的点,连接GH,若线段GH与EF的夹角为45°,则GH的长为( )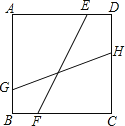
A.
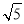 B.
B.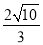 C.
C. 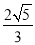 D.
D. 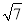
-
科目: 来源: 题型:
查看答案和解析>>【题目】媒体报道,近期“手足口病”可能进入发病高峰期,某校根据《学校卫生工作条例》,为预防“手足口病”,对教室进行“薰药消毒”.已知药物在燃烧及释放过程中,室内空气中每立方米含药量y(毫克)与燃烧时间x(分钟)之间的关系如图所
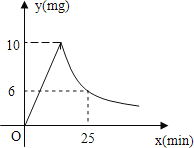
示(即图中线段OA和双曲线在A点及其右侧的部分),根据图象所示信息,解答下列问题:
(1)写出从药物释放开始,y与x之间的函数关系式及自变量的取值范围;
(2)据测定,当空气中每立方米的含药量低于2毫克时,对人体无毒害作用,那么从消毒开始,至少在多长时间内,师生不能进入教室?
相关试题

