搜索
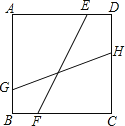
【题目】如图，正方形ABCD的边长为2，点E、F分别为边AD、BC上的点，EF=
，点G、H分别为AB、CD边上的点，连接GH，若线段GH与EF的夹角为45°，则GH的长为（ ）
A． B.
C. 
D. 
参考答案：
【答案】B．
【解析】
试题如图，过点B作BK∥EF交AD于K，作BM∥GH交CD于M，则BK=EF=
，BM=GH，
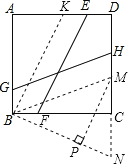
∵线段GH与EF的夹角为45°，
∴∠KBM=45°，
∴∠ABK+∠CBM=90°-45°=45°，
作∠MBN=45°交DC的延长线于N，则∠CBN+∠CBM=45°，
∴∠ABK=∠CBN，
在△ABK和△CBN中，
，
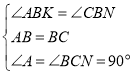∴△ABK≌△CBN（ASA），
∴BN=BK，AK=CN，
在Rt△ABK中，AK=
，
过点M作MP⊥BN于P，
∵∠MBN=45°，
∴△BMP是等腰直角三角形，
设GH=BM=x，则BP=MP=
BM=
，
∵tan∠N=
，
∴
，
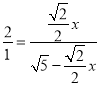解得x=
，
所以GH=．
故选B．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读材料：
在平面直角坐标系中，二元一次方程x-y=0的一个解
可以用一个点（1，1）表示，二元一次方程有无数个解，以方程x-y=0的解为坐标的点的全体叫作方程x-y=0的图象。一般地，在平面直角坐标系中，任何一个二元一次方程的图象都是一条直线，我们可以把方程x-y=0的图象称为直线x-y=0。直线x-y=0把坐标平面分成直线上方区域，直线上，直线下方区域三部分，如果点M（x0，y0）的坐标满足不等式x-y≤0，那么点M（x0，y0）就在直线x-y=0的上方区域内。特别地，x=k（k为常数）表示横坐标为k的点的全体组成的一条直线，y=m（m为常数）表示纵坐标为m的点的全体组成的一条直线。
请根据以上材料，探索完成以下问题：
（1）已知点A（2，1）、B（
，
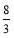）、C（
，
）、D（4，
），其中在直线3x-2y=4上的点有 ；请再写出直线3x-2y=4上一个点的坐标 ；（2）已知点P（x，y）的坐标满足不等式组
，则所有的点P组成的图形的面积是 ；（3）已知点P（x，y）的坐标满足不等式组
,请在平面直角坐标系中画出所有的点P组成的图形（涂上阴影），并直接写出上述图形的面积 。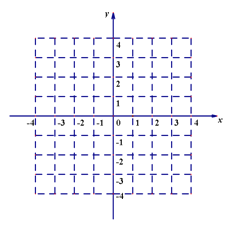
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知在直角梯形AOBC中，AC∥OB，CB⊥OB，OB=18，BC=12，AC=9，对角线OC、AB交于点D，点E、F、G分别是CD、BD、BC的中点，以O为原点，直线OB为x轴建立平面直角坐标系，则G、E、D、F四个点中与点A在同一反比例函数图象上的是（ ）
A. 点G B. 点E C. 点D D. 点F
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在方格纸中（小正方形的边长为1），反比例函数y=
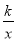与直线的交点A、B均在格点上，根据所给的直角坐标系（O是坐标原点），解答下列问题：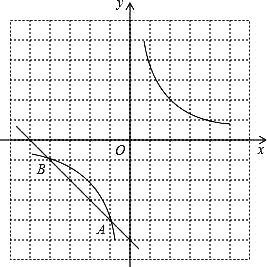
（1）分别写出点A、B的坐标后，把直线AB向右平移5个单位，再向上平移5个单位，画出平移后的直线A′B′；
（2）若点C在函数y=
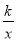的图象上，△ABC是以AB为底的等腰三角形，请写出点C的坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】媒体报道，近期“手足口病”可能进入发病高峰期，某校根据《学校卫生工作条例》，为预防“手足口病”，对教室进行“薰药消毒”．已知药物在燃烧及释放过程中，室内空气中每立方米含药量y（毫克）与燃烧时间x（分钟）之间的关系如图所
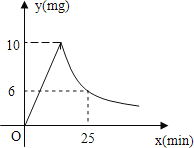
示（即图中线段OA和双曲线在A点及其右侧的部分），根据图象所示信息，解答下列问题：
（1）写出从药物释放开始，y与x之间的函数关系式及自变量的取值范围；
（2）据测定，当空气中每立方米的含药量低于2毫克时，对人体无毒害作用，那么从消毒开始，至少在多长时间内，师生不能进入教室？
-
科目： 来源： 题型：
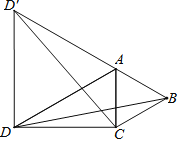
查看答案和解析>>【题目】如图，在△ACD中，AD=9，CD=
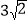,△ABC中，AB=AC，若∠CAB=60°,∠ADC=30°,在△ACD外作等边△ADD′（1）求证：BD=CD′
（2）求BD的长.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，∠B =∠C，点D、E分别是边AB、AC上的点，PD平分∠BDE交BC于H，PE平分∠DEC交BC于G，DQ平分∠ADE交PE延长线于Q。
（1）∠A+∠B+∠C+∠P +∠Q = °；
（2）猜想∠P与∠A的数量关系，并证明你的猜想；
（3）若∠EGH =112°，求∠ADQ 的大小。
相关试题
